Неравенства с одной переменной (основные понятия)
Неравенством с одной переменной называется неравенство, содержащее одну независимую переменную. Неравенства с переменными называют иногда функциональными неравенствами.
Пусть дано неравенство с одной переменной (вместо знака могут быть знаки 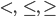 ). Областью определения неравенства называется пересечение областей определения функций
). Областью определения неравенства называется пересечение областей определения функций  и
и 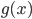 .
.
Решением неравенства называется всякое значение переменной, при котором исходное неравенство с переменной обращается в верное числовое неравенство. Решить неравенство с переменной — значит найти все его решения или доказать, что решений нет. Два неравенства с одной переменной называются равносильными (эквивалентными), если решения этих неравенств совпадают; в частности, неравенства равносильны, если они не имеют решений.
При решении неравенств пользуются следующими основными теоремами о равносильности неравенств:
1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное исходному.
2. Если к обеим частям неравенства прибавить (или вычесть) любую функцию 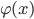 , то получится неравенство, равносильное исходному при условии, что области определения полученного и исходного неравенств совпадают.
, то получится неравенство, равносильное исходному при условии, что области определения полученного и исходного неравенств совпадают.
3. Если обе части неравенства умножить (или разделить) на любую функцию 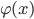 , сохраняющую постоянный знак и отличную от нуля, то при получается неравенство, равносильное исходному, а при
, сохраняющую постоянный знак и отличную от нуля, то при получается неравенство, равносильное исходному, а при 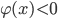 равносильным исходному будет неравенство противоположного смысла (предполагается, что области определения полученного и исходного неравенств совпадают). Таким образом, можем записать:
равносильным исходному будет неравенство противоположного смысла (предполагается, что области определения полученного и исходного неравенств совпадают). Таким образом, можем записать:
если ;
если ;
если 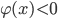 ;
;
если 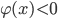 .
.
Замечание. На практике при применении 2 и 3 теорем чаще всего вместо функции 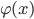 берется ее частный случай — отличная от нуля константа.
берется ее частный случай — отличная от нуля константа.
Пример. и равносильны по теореме 1. Неравенство 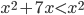 равносильно неравенству
равносильно неравенству 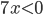 по теореме 2, которое, в свою очередь, равносильно неравенству
по теореме 2, которое, в свою очередь, равносильно неравенству 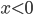 по теореме 3. Неравенство
по теореме 3. Неравенство 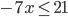 равносильно неравенству
равносильно неравенству 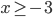 по теореме 3, т. к. обе части неравенства
по теореме 3, т. к. обе части неравенства 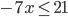 можно разделить на отрицательное число (-7), изменив при этом знак
можно разделить на отрицательное число (-7), изменив при этом знак  на знак
на знак 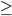 .
.






