При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой дроби вычитают числитель второй дроби) и оставляют тот же знаменатель. Полученную дробь, если это возможно, сокращают.
Например, 5/11+3/11=(5+3)/11=8/11; 6/17-2/17=(6-2)/17=4/17.
При сложении (вычитании) дробей с различными знаменателями предпочтительнее предварительно привести их к наименьшему общему знаменателю. Например,
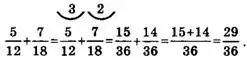
Замечание 1. При сложении (вычитании) дробей не обязательно приводить дроби к наименьшему общему знаменателю, а можно приводить к общему знаменателю, однако в этом случае приходится иметь дело с большими по величине числами. Например,
![]()
Как видим, предпочтительнее приводить дроби именно к наименьшему общему знаменателю, а не просто к общему знаменателю.
При сложении смешанных дробей нужно сложить отдельно целые части и дробные части. Например:
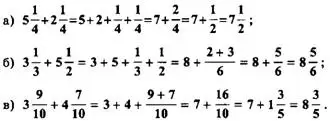
При вычитании смешанных дробей следует различать следующие случаи:
а) дробная часть уменьшаемого больше или равна дробной части вычитаемого; в этом случае из целой части уменьшаемого вычитают целую часть вычитаемого, а из дробной части уменьшаемого — дробную часть вычитаемого, например,
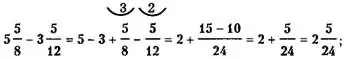
б) дробная часть уменьшаемого меньше дробной части вы¬читаемого (например, ); в этом случае одну из единиц
целой части уменьшаемого нужно заменить равной ей дробью. Например:
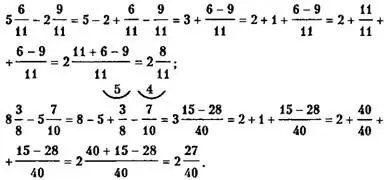
Замечание 2. При сложении (вычитании) смешанных дробей можно предварительно представить их в виде неправильной дроби, а затем производить сложение (вычитание). Например:

Этим способом обычно пользуются тогда, когда имеют дело с небольшими по величине числами.
Замечание 3. Действие вычитания дробей может привести к понятию отрицательной дроби, которая получается, если перед положительной дробью поставить знак "минус". Используя отрицательные дроби, можно при вычитании смешанных дробей поступать так:
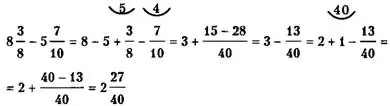
При вычитании дробей можно не использовать единицу, то есть решение вышеприведенного примера записывать так:
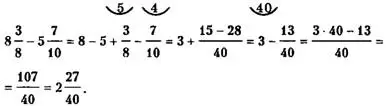
Отметим, что приведенную разность дробей можно было бы находить и с использованием неправильных дробей, а именно:
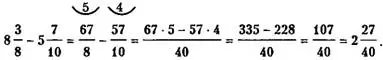
Для данного конкретного примера вычисления с использованием неправильных дробей, как видим, получаются более громоздкими.
Сложение и вычитание дробей






