При сложении (вычитании) натуральных чисел столбиком надо
• подписать одно число под другим так, чтобы единицы были под единицами, десятки — под десятками, сотни — под сотнями и т.д.;
• сложить (вычесть) числа поразрядно, начиная с разряда единиц.
Задание 1. Выполните действие: а) 346+ 458; б)2463-378.
Решение.
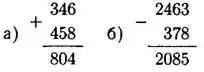
Ответ: а) 804; 6)2085.
При сложении (вычитании) десятичных дробей надо
• уравнять в этих дробях количество знаков после запятой;
• записать числа друг под другом так, чтобы запятая была под запятой;
• выполнить сложение (вычитание), не обращая внимания на запятую;
• поставить в ответе запятую под запятой в данных дробях.
Задание 2. Выполните действие: а) 13,28 + 5,145; б) 3,6 - 1,551.
Решение.
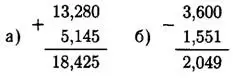
Ответ: а) 18,425; 6)2,049.
Задание 3. Выполните действие: а) 24,2 + 0,867; 6) 448,32 - 51,435; в) 451 -2,553.
Решение.

Ответ: а) 25,067; б)396,885; в) 448,447.
При сложении (вычитании) обыкновенных дробей надо
• привести дроби к наименьшему общему знаменателю;
• сложить (вычесть) числители, результат записать в числитель;
• в знаменатель записать найденный наименьший общий знаменатель.
Задание 4. Выполните действие: а)  б)
б) 
Решение.
а) Приведём дроби  и
и  к наименьшему общему знаменателю. Для этого умножим числители и знаменатели этих дробей на дополнительные множители 5 и 3 соответственно:
к наименьшему общему знаменателю. Для этого умножим числители и знаменатели этих дробей на дополнительные множители 5 и 3 соответственно:

б) Приведём дроби  и
и  к наименьшему общему знаменателю. Для этого умножим числители и знаменатели этих дробей на дополнительные множители 2 и 3 соответственно:
к наименьшему общему знаменателю. Для этого умножим числители и знаменатели этих дробей на дополнительные множители 2 и 3 соответственно:

Ответ: а)  б)
б) 
Задание 5. Выполните действие 
Решение.
Для приведения исходных дробей к наименьшему общему знаменателю найдём НОК (наименьшее общее кратное) чисел 18 и 24. Разложим 18 и 24 на простые множители:
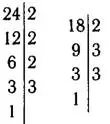
Отсюда НОК 

Ответ: 
Задание 6. Выполните действия 
Решение.
Для упрощения вычислений поменяем местами  и
и  :
:

Ответ: 
Задание 7. Выполните действие 
Решение.

Ответ: 







