Не во всякий четырёхугольник можно вписать окружность.
Не вокруг любого четырёхугольника можно описать окружность.
В любом описанном четырёхугольнике суммы противоположных сторон равны.  (см. рис.1).
(см. рис.1).
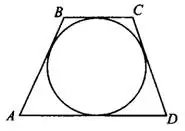
Рис.1
Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.
В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.
 (см. рис. 2).
(см. рис. 2).
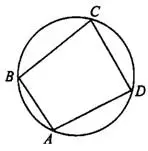
Рис.2
Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
В любой правильный многоугольник можно вписать окружность, то есть построить такую окружность, которая касается всех сторон правильного многоугольника (имеет с каждой стороной ровно одну общую точку). В этом случае говорят, что многоугольник описан вокруг окружности. Пример для пятиугольника приведён на рисунке 3.
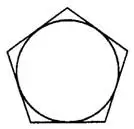
Рис.3
Вокруг любого правильного многоугольника можно описать окружность. То есть построить такую окружность, которая проходит через все вершины правильного многоугольника (см. рис.4). В этом случае говорят, что многоугольник вписан в окружность.
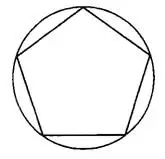
Рис.4
Задача 1. Около четырёхугольника описана окружность (см. рис. 5). Найдите величину угла А этого четырёхугольника. Ответ дайте в градусах.
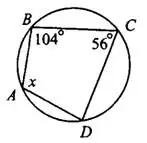
Рис.5
Решение.
Сумма противоположных углов вписанного четырёхугольника равна 180°.
 .
.
Ответ: 124.
Задача 2. В четырёхугольник вписана окружность (см. рис.6).  . Найдите
. Найдите 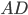 .
.
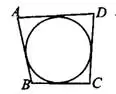
Рис.6
Решение.
Четырёхугольник 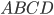 вписан в окружность. Значит,
вписан в окружность. Значит,  , то есть
, то есть  , откуда
, откуда  .
.
Ответ: 13.







