Формулы сокращённого умножения. Готовимся к ОГЭ по математике. Модуль 1. Урок 16

Следует запомнить три формулы сокращённого умножения.
• Квадрат суммы: 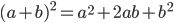$\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}$.
• Квадрат разности: 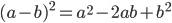$\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}$.
• Разность квадратов: 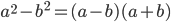$\displaystyle a^{2}-b^{2}=(a-b)(a+b)$.
Например:
$\displaystyle (2c+3)^{2}=(2c)^{2}+2\cdot 2c\cdot 3+3^{2}=4c^{2}+12c+9;$
$\displaystyle (3k-1)^{2}=(3k)^{2}-2\cdot 3k\cdot 1+1^{2}=9k^{2}-6k+1;$
$\displaystyle t^{2}-25=t^{2}-5^{2}=(t-5)(t+5).$
Пример 1. Сократите дробь $\displaystyle \frac{x^{2}+2x+1}{x+1},\; x\neq -1.$
Решение.
$\displaystyle \frac{x^{2}+2x+1}{x+1}=\frac{x^{2}+2\cdot x\cdot 1+1^{2}}{x+1}=\frac{(x+1)^{2}}{x+1}=x+1.$
Ответ: $\displaystyle x+1.$

Пример 2. Сократите дробь $\displaystyle \frac{a^{2}-9}{a+3},\; a\neq -3.$
Решение.
$\displaystyle \frac{a^{2}-9}{a+3}=\frac{a^{2}-3^{2}}{a+3}=\frac{(a-3)(a+3)}{a+3}=a-3.$
Ответ: $\displaystyle a-3.$