График функции, заданной формулой вида  или
или  , где
, где 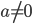 , — парабола. Вершина параболы находится в точке с абсциссой, равной
, — парабола. Вершина параболы находится в точке с абсциссой, равной  , и в зависимости от знака параметра
, и в зависимости от знака параметра  и знака выражения
и знака выражения  график может принимать различный вид (см. рис. 1).
график может принимать различный вид (см. рис. 1).
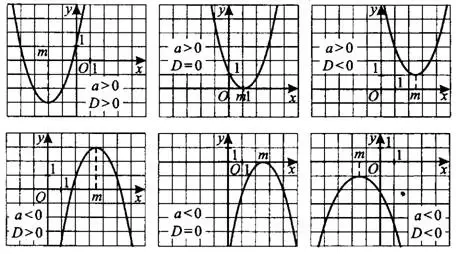
Рис. 1
При ветви параболы направлены вверх, при 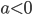 — вниз. Знак дискриминанта
— вниз. Знак дискриминанта 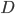 показывает, пересекает ли парабола ось абсцисс. При парабола пересекает ось абсцисс дважды, при
показывает, пересекает ли парабола ось абсцисс. При парабола пересекает ось абсцисс дважды, при  — один раз (вершина параболы лежит на оси абсцисс). При
— один раз (вершина параболы лежит на оси абсцисс). При  парабола не пересекает ось абсцисс.
парабола не пересекает ось абсцисс.
Пример 1. Установите соответствие между графиками функций (см. рис. 2) и формулами, которые их задают.
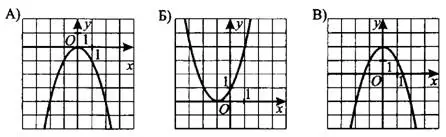
Рис. 2
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
Решение. Все три графика — параболы, то есть заданы формулами вида  или
или  .
.
На графике А ветви параболы направлены вниз, значит, параметр 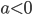 . Этому условию отвечают формулы 1 и 4, но так как график А проходит через точку плоскости с координатами (0;0), а график, заданный формулой 1, через неё не проходит (при
. Этому условию отвечают формулы 1 и 4, но так как график А проходит через точку плоскости с координатами (0;0), а график, заданный формулой 1, через неё не проходит (при  ), то графику А соответствует формула 4. На графике Б ветви параболы направлены вверх, , и он может быть задан формулой 2 или 3, но так как вершина параболы лежит на оси
), то графику А соответствует формула 4. На графике Б ветви параболы направлены вверх, , и он может быть задан формулой 2 или 3, но так как вершина параболы лежит на оси  в точке с абсциссой
в точке с абсциссой  , то
, то  . Формула 3 не подходит, так как для неё
. Формула 3 не подходит, так как для неё  . Графику Б соответствует формула 2:
. Графику Б соответствует формула 2:  .
.
На графике В ветви параболы направлены вниз, 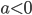 , и ему могут соответствовать формулы 1 и 4. Так как
, и ему могут соответствовать формулы 1 и 4. Так как  , то формула 4 не подходит (в ней
, то формула 4 не подходит (в ней  ), следовательно, график В задаёт формула 1.
), следовательно, график В задаёт формула 1.
Ответ: А-4; Б-2; В-1.
Замечание. Для параболы при проверке соответствия графика одной из нескольких формул удобно использовать сравнение координат вершины параболы, изображённой на графике, и координат вершин парабол, задаваемых формулами. Если эти координаты для двух формул совпадают, следует
выбирать ещё одну дополнительную точку графика для проверки.







