Линейные неравенства. Готовимся к ОГЭ по математике. Модуль 1. Урок 27

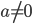Линейным неравенством называется неравенство вида $\displaystyle ax+b>0,\; ax+b<0,\; ax+b\geq 0,\; ax+b\leq 0$ , где $x$ — переменная, $a$ и $b$ — некоторые числа, причём $\displaystyle a\neq 0$ . Для решения неравенства $\displaystyle ax+b>0$ сначала перенесём слагаемое $b$ в правую часть: $\displaystyle ax>-b$ . Далее разделим обе части неравенства на $a$ . При этом следует учитывать знак $a$ :
• если $\displaystyle a>0$ , то при делении неравенство сохраняет знак: $\displaystyle x>-\frac{b}{a}$ , то есть $\displaystyle x\in \left ( -\frac{b}{a};+\infty \right );$
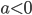• если $\displaystyle a<0$ , то при делении неравенство меняет знак на противоположный: $\displaystyle x<-\frac{b}{a}$ то есть $\displaystyle x\in \left ( -\infty; -\frac{b}{a} \right ).$ Аналогично решаются неравенства $\displaystyle ax+b<0,\; ax+b\geq 0,ax+b\leq 0.$
Пример 1. Решите неравенство $\displaystyle 5x-3<7x-17$ .
Решение.
Перенесём в левую часть все слагаемые, содержащие переменную, а в правую — свободные члены: $\displaystyle 5x-3<7x-17$ , $\displaystyle -2x<-14.$ Разделим обе части на (—2), знак неравенства при этом изменится на противоположный: $\displaystyle x>7$ (см. рис. 1).