Правила раскрытия скобок:
• Если перед скобками стоит знак «+», то при раскрытии скобок все слагаемые остаются без изменений. Например, 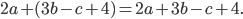
• Если перед скобками стоит знак «—», то при раскрытии скобок каждое слагаемое меняет знак на противоположный. Например, 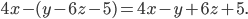
• Если перед скобками (или после скобок) стоит множитель, то при раскрытии скобок каждое слагаемое умножается на этот множитель. При подсчёте этих произведений следует учитывать как знак множителя за скобками, так и знаки слагаемых внутри скобок.
Рассмотрим два примера:


Пример 1. Упростите выражение  и найдите его значение при
и найдите его значение при  .
.
Решение.
 Подставляя вместо
Подставляя вместо  и
и  указанные в условии числа, получаем
указанные в условии числа, получаем 
Ответ:  .
.
Пример 2. Упростите выражение  и найдите его значение при
и найдите его значение при  .
.
Решение.
 . Подставляя вместо
. Подставляя вместо  и
и  указанные в условии числа, получаем
указанные в условии числа, получаем 
Ответ: 
Если требуется раскрыть произведение, состоящее из нескольких скобок, то скобки следует раскрывать поочерёдно. Например:


В этом примере мы сначала раскрыли первые скобки  , а затем вторые скобки
, а затем вторые скобки  . Но можно было сделать и по-другому, начав с раскрытия вторых скобок:
. Но можно было сделать и по-другому, начав с раскрытия вторых скобок:


Пример 3. Упростите выражение  и найдите его значение при
и найдите его значение при 
Решение.

Подставляя  , получаем
, получаем 
Ответ: 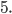
Правила раскрытия скобок. Готовимся к ОГЭ по математике. Модуль 1. Урок 15







