Прямоугольный треугольник. Готовимся к ОГЭ по математике. Модуль 2. Урок 47

Часто углы измеряют не в градусах, а в радианах.
$\displaystyle 1^{\circ}=\frac{\pi }{180}$ (радиан), впрочем, единицу измерения часто опускают.
$\displaystyle 30^{\circ}=30\cdot \frac{\pi }{180}=\frac{\pi }{6};\; 60^{\circ}=\frac{\pi }{3};\; 90^{\circ}=\frac{\pi }{2};\; 180^{\circ}=\pi$ (радиан) и т. д.

Прямоугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90°.
Сторона, лежащая против угла 90° (прямого угла), называется гипотенузой, две другие — катетами.
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.
Например, 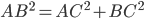$\displaystyle AB^{2}=AC^{2}+BC^{2}$ (см. рис.1).

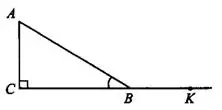
Рис.1

Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Например, $\displaystyle \sin \angle B=\frac{AC}{AB},\; \cos \angle B=\frac{CB}{AB}$ (см. рис.1).
Для любого угла можно найти его синус и косинус, они зависят только от градусной меры угла.
Синус угла равен синусу смежного с ним угла ($\displaystyle \sin \angle ABK=\sin \angle CBA$).
Косинусы смежных углов — противоположные числа ($\displaystyle \cos \angle ABK=-\cos \angle CBA$).

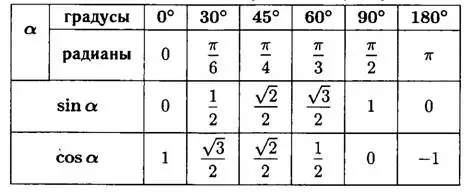
Значения синуса и косинуса некоторых углов

В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы. На рисунке 2 в $\displaystyle \bigtriangleup ABC$ $\displaystyle \angle C=90^{\circ},\angle A=30^{\circ}$, значит, $\displaystyle BC=\frac{1}{2}AB$.

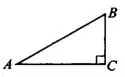
Рис.2

Задача 1. Найдите $\displaystyle \cos 120^{\circ}$.
Решение.
Так как угол в $\displaystyle \cos 120^{\circ}$ смежен с углом в $\displaystyle \cos 60^{\circ} \; (120^{\circ}+60^{\circ}=180^{\circ})$, то $\displaystyle \cos 120^{\circ}=-\cos 60^{\circ}=-\frac{1}{2}=-0,5$.
Ответ: -0,5.
Задача 2. Найдите сторону 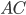$AC$ треугольника $ABC$, если $\displaystyle \angle ACB=90^{\circ},AB=5,BC=4$ (см. рис.3).

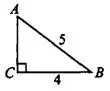
Рис.3

Решение.
По теореме Пифагора, 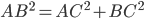$\displaystyle AB^{2}=AC^{2}+BC^{2}$, откуда $\displaystyle AC^{2}=AB^{2}-BC^{2}=5^{2}-4^{2}=9,\; AC=\sqrt{9}=3$.
Ответ: 3.