Системы неравенств. Готовимся к ОГЭ по математике. Модуль 1. Урок 30

Система обозначается знаком {. Решением системы неравенств являются те значения, которые одновременно являются решением всех неравенств системы. При решении системы неравенств на координатной прямой заштриховывается промежуток, который соответствует ответу.
Как и в предыдущих случаях, границы промежутка обозначаются белыми «выколотыми» точками, если они не входят в сам промежуток. В противном случае они обозначаются чёрными «сплошными» точками.
Пример 1. Решите систему неравенств $\displaystyle \left\{\begin{matrix} 3x+5>0,\\ 3x-9\leq 0. \end{matrix}\right.$
На какой из координатных прямых изображено множество решений системы (см. рис. 1)?

Рис.1

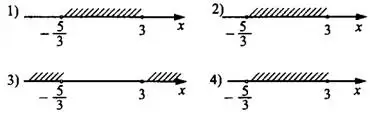
Решение.
1) Решим первое неравенство: $\displaystyle 3x>-5,\; x>-\frac{5}{3}.$
2) Решим второе неравенство: $\displaystyle 3x-9\leq 0,\; 3x\leq 9,\; x\leq 3.$

Рис.2

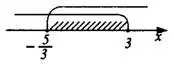
3) На координатной прямой (см. рис. 2) обозначены дугами решения каждого из неравенств. Заштрихуем их обшую часть. При этом обратим внимание, что число 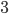$3$ входит в решение, а $\displaystyle -\frac{5}{3}$ - нет. Из предложенных в условии подходит координатная прямая под номером 4.
Ответ: 4.