Рассмотрим прямоугольную систему координат 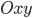 (см. рис. 1).
(см. рис. 1).
Длина отрезка  , для которого известны координаты его концов
, для которого известны координаты его концов 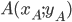 и
и 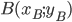 , определяется по формуле
, определяется по формуле 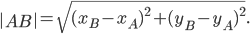
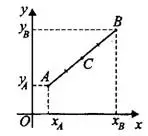
Координаты середины отрезка вычисляются по формулам: 
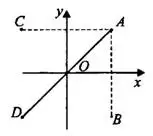
Если точки  и
и  симметричны относительно оси
симметричны относительно оси  (оси абсцисс), то их ординаты противоположны (см. рис. 2), а абсциссы равны:
(оси абсцисс), то их ординаты противоположны (см. рис. 2), а абсциссы равны:  ,
,  .
.
Если точки  и
и  симметричны относительно оси
симметричны относительно оси  , то их абсциссы противоположны, а ординаты равны:
, то их абсциссы противоположны, а ординаты равны:  ,
,  .
.
Если точки  и
и  симметричны относительно начала координат, то их координаты противоположны:
симметричны относительно начала координат, то их координаты противоположны:  ,
,  .
.
Задача 1. Найдите расстояние от точки  с координатами (12;-5) до начала координат (см. рис. 3).
с координатами (12;-5) до начала координат (см. рис. 3).
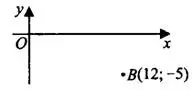
Решение.
Начало координат находится в точке  . Расстояние от
. Расстояние от  до
до  равно
равно 
Ответ: 13.
Задача 2. Найдите абсциссу точки, симметричной точке  относительно оси
относительно оси  (см. рис. 4).
(см. рис. 4).
Решение.
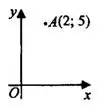
Точке  симметрична точка
симметрична точка  (см. рис. 5). Абсцисса точки
(см. рис. 5). Абсцисса точки  равна —2.
равна —2.
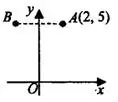
Ответ: -2.







