Напомним, что трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
Площадь трапеции равна половине произведения суммы оснований 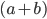 на высоту
на высоту 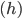 :
:
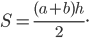
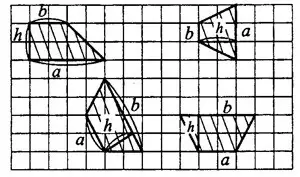
На рисунке 1 приведены чертежи некоторых трапеций, у каждой из которых показаны основания  и
и  и высота
и высота 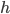 .
.
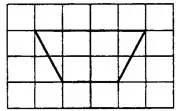
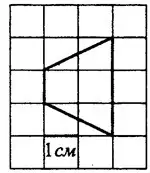
Задача 1. На клетчатой бумаге с клетками размером 1см х 1см изображена трапеция (см. рис. 2). Найдите её площадь в квадратных сантиметрах.
Решение.
1-й способ.
Площадь трапеции равна половине произведения суммы оснований на высоту. Обозначим трапецию 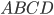 . Проведём из точки
. Проведём из точки 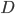 высоту
высоту  к основанию
к основанию  . По рисунку 3 видно, что высота равна 2 см, основания
. По рисунку 3 видно, что высота равна 2 см, основания  = 4 см,
= 4 см,  = 2 см.
= 2 см.
Площадь трапеции  (см²).
(см²).
Ответ: 6.
2-й способ.
Разобьём трапецию на три части — два прямоугольных треугольника и квадрат. Сторона квадрата 2, площадь квадрата  , катеты каждого из прямоугольных треугольников 1 и 2, площадь каждого из прямоугольных треугольников равна половине произведения катетов,
, катеты каждого из прямоугольных треугольников 1 и 2, площадь каждого из прямоугольных треугольников равна половине произведения катетов,  . Получаем, что площадь трапеции
. Получаем, что площадь трапеции  (см²).
(см²).
Ответ: 6.
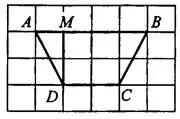
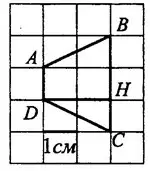
Задача 2. На клетчатой бумаге с клетками размером 1 см х 1 см изображена трапеция (см. рис. 4). Найдите её площадь в квадратных сантиметрах.
Решение.
Обозначим трапецию 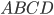 . Проведём высоту
. Проведём высоту  . На рисунке 5 видно, что высота равна 2 см, основание
. На рисунке 5 видно, что высота равна 2 см, основание 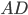 = 1 см,
= 1 см, 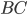 = 3 см.
= 3 см.
Площадь трапеции равна произведению полусуммы оснований на высоту:  (см²).
(см²).
Ответ: 4.
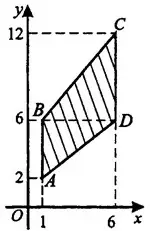
Задача 3. Найдите площадь трапеции, вершины которой имеют координаты (1; 2), (1; 6), (6; 12), (6; 6) (см. рис. 6).
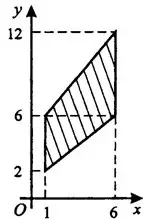
Решение.
1-й способ.
Площадь трапеции равна половине произведения суммы оснований на высоту. Обозначим трапецию 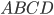 (см. рис. 7). Проведём из точки
(см. рис. 7). Проведём из точки  перпендикуляр к
перпендикуляр к  . Этим перпендикуляром будет
. Этим перпендикуляром будет  . Высота
. Высота  = 6 — 1 = 5, основания трапеции
= 6 — 1 = 5, основания трапеции  и
и  равны 4 и 6 соответственно. Найдём площадь трапеции
равны 4 и 6 соответственно. Найдём площадь трапеции 
Ответ: 25.
2-й способ.
Разобьём трапецию на два прямоугольных треугольника  и
и  (см. рис. 7). Площадь прямоугольного треугольника
(см. рис. 7). Площадь прямоугольного треугольника  с катетами
с катетами  = 4 и
= 4 и  = 5 равна половине произведения катетов, то есть 4 · 5 : 2 = 10. Площадь прямоугольного треугольника
= 5 равна половине произведения катетов, то есть 4 · 5 : 2 = 10. Площадь прямоугольного треугольника  с катетами
с катетами  = 5 и
= 5 и  = 6 равна половине произведения катетов, то есть 6 · 5 : 2 = 15. Площадь трапеции равна сумме площадей треугольников
= 6 равна половине произведения катетов, то есть 6 · 5 : 2 = 15. Площадь трапеции равна сумме площадей треугольников  и
и  . Получим
. Получим  = 10 + 15 = 25.
= 10 + 15 = 25.
Ответ: 25.







