При увеличении всех линейных измерений тела в 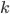 раз площадь поверхности этого тела увеличивается в
раз площадь поверхности этого тела увеличивается в 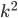 раз, а объём этого тела — в
раз, а объём этого тела — в 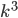 раз. Например, при увеличении радиуса шара в 5 раз площадь его поверхности увеличится в 25 раз, а объём — в 125 раз.
раз. Например, при увеличении радиуса шара в 5 раз площадь его поверхности увеличится в 25 раз, а объём — в 125 раз.
Объём параллелепипеда, призмы, цилиндра и конуса прямо пропорционален высоте и площади основания.
Задача 1. Во сколько раз увеличится объём куба, если его рёбра увеличить в 4 раза?
Решение.
Объём куба прямо пропорционален третьей степени его ребра, поэтому объём увеличится в 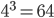 раза.
раза.
Ответ: 64.
Задача 2. Во сколько раз увеличится объём правильного тетраэдра, если все его рёбра увеличить в три раза?
Решение.
При увеличении всех линейных размеров тетраэдра в 3 раза его объём увеличится в 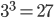 раз.
раз.
Ответ: 27.
Задача 3. Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 2,5 раза?
Решение.
Объём конуса прямо пропорционален площади основания. Площадь основания равна 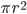 , то есть прямо пропорциональна квадрату радиуса. Таким образом, при увеличении радиуса основания в 2,5 раза объём увеличится в
, то есть прямо пропорциональна квадрату радиуса. Таким образом, при увеличении радиуса основания в 2,5 раза объём увеличится в 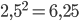 раз.
раз.
Ответ: 6,25.
Увеличение и уменьшение геометрических тел. Готовимся к ЕГЭ по математике. Геометрия. Урок 31







