Переменные величины и функции, их обозначение. Решение задач. Практикум по математическому анализу. Урок 2

Пример 1. Определить и построить на числовой оси области изменения переменных $x,t$ и $a$ , заданные следующими неравенствами:
$\displaystyle 1)\: x^{2}\leq 4;\: 2)\: \left | t-1 \right |>0;\: 3)\: -9\leq 1-2\alpha <5.$
Решение. 1) Извлекая квадратный корень из обеих частей первого неравенства, получим $\displaystyle \left | x \right |\leq 2$ . Отсюда следует, что $\displaystyle -2\leq x\leq 2$ . Эти неравенства и определяют собой область изменения переменной $x$ , т. е. совокупность принимаемых ею числовых значений. Она представляет закрытый интервал или отрезок [—2; 2]. Построим этот отрезок на числовой оси $Ox$ (рис. 1); он будет симметричен относительно начальной точки $x=0$ .

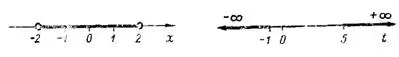
Рис. 1 Рис. 2

2) Избавляясь от знака абсолютной величины в неравенстве, содержащем $t$ , получим два неравенства: $\displaystyle t-2<-3$ и $\displaystyle t-2>3$ . Разрешая их относительно $t$ , найдем $t<-1$ и $t>5$ . Следовательно, область изменения переменной $t$ (рис. 2) состоит из двух бесконечных открытых интервалов $\displaystyle (-\infty ;-1)$ и $\displaystyle (5;+\infty)$ .
3) Решаем неравенства, содержащие $\displaystyle \alpha$ . Вычитая из всех частей неравенств по единице и затем деля их на —2, получим $\displaystyle -10\leq -2\alpha <4,\; -2<\alpha \leq 5.$ Следовательно, область изменения переменной а (рис. 3) представляет полуоткрытый интервал $\displaystyle (-2;5]$ .
Пример 2. Вычислить частное значение функции:
1) $\displaystyle f(x)=\sqrt{x^{2}-5x+4}$ а) при $x=0$ ; б) при $x=a+1$ ;
2) $\displaystyle \phi (x)=2\arcsin x+arctg\: 2x$ при $\displaystyle x=-\frac{1}{2}$ ;
3) $\displaystyle y=x^{2}\arccos \frac{x}{2}-3x\: arcctg\: x$ при $\displaystyle x=-1$ .
Решение. 1a) Подставляя значение $x=0$ , получим соответствующее частное значение функции $\displaystyle f(x)$ : $\displaystyle f(0)=\sqrt{0^{2}-5\cdot 0+4}=\sqrt{4}=2$ . Здесь взято арифметическое значение корня, а не ±2. Вообще в математическом анализе рассматриваются только однозначные функции, которые могут иметь только одно значение при каждом значении аргумента.
1б) При $x=a+1$ частное значение функции $\displaystyle f(x)$ будет $\displaystyle f(a+1)=\sqrt{(a+1)^{2}-5\cdot (a+1)+4}=\sqrt{a^{2}-3a}$ .
2) Частное значение функции $\displaystyle \phi (x)$ при $\displaystyle x=-\frac{1}{2}$ :
$\displaystyle \phi \left ( -\frac{1}{2} \right )=2\arcsin \left ( -\frac{1}{2} \right )+arctg(-1)=2\left ( -\frac{\pi }{6} \right )+\left ( -\frac{\pi }{4} \right )=-\frac{7}{12}\pi$ .
Здесь учтено, что $\displaystyle \arcsin x$ и $\displaystyle arctg \: x$ — однозначные функции, изменяющиеся между $\displaystyle -\frac{\pi }{2}$ и $\displaystyle \frac{\pi }{2}$ (поскольку $\displaystyle -\frac{\pi }{2}\leq \arcsin x\leq \frac{\pi }{2};\; -\frac{\pi }{2}<arctg\: x< \frac{\pi }{2}$ ). При $\displaystyle x>0$ их значения берутся в первой четверти, а при $\displaystyle x<0$ — в четвертой.
3) При $\displaystyle x=-1$ частное значение функции $y$ будет
$\displaystyle y(-1)=(-1)^{2}\arccos\left ( -\frac{1}{2} \right )-3(-1)arcctg(-1)=\frac{2}{3}\pi +\frac{9}{4}\pi =\frac{35}{12}\pi ,$
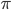так как $\displaystyle \arccos x$ и $\displaystyle arcctg x$ — однозначные функции, изменяющиеся от $0$ до $\displaystyle \pi$ (поскольку $\displaystyle 0\leq \arccos x\leq \pi ;\; 0<arcctg\: x<\pi$ ). При $\displaystyle x>0$ их значения берутся в первой четверти, а при $\displaystyle x<0$ — во второй.