Прямая в пространстве. Решения типовых задач. Часть 2

Решения типовых задач по теме "Задание прямой в пространстве". Часть 2
Задача №1. Определить косинус угла между двумя пря­мыми:

$$\left\{\begin{matrix} 3x-4y-2z=0,\\ 2x+y-2z=0 \end{matrix}\right.$$

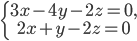
и

$$\left\{\begin{matrix} 4x+y-6z-2=0,\\ y-3z-2=0. \end{matrix}\right.$$

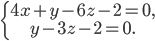
Задача №2. Проверить, лежат ли прямые
а)

$$\left\{\begin{matrix} 2x-3z+2=0,\\ 2y-z-6=0, \end{matrix}\right.$$

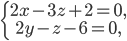
и

$$\left\{\begin{matrix} x-12z+49=0,\\ 4x-37z+148=0; \end{matrix}\right.$$

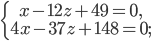
б)

$$\left\{\begin{matrix} x=3z-1,\\ y=-5z+7, \end{matrix}\right.$$

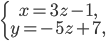
и

$$\left\{\begin{matrix} y=2x-5,\\ z=7x+2 \end{matrix}\right.$$

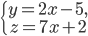
в одной плоскости.
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Найти уравнения прямой, пересекающей пря­мую

$$\frac{x-1}{1}=\frac{y+3}{0}=\frac{z-2}{-2}$$

,
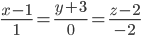
проходящей через точку А (2;-2;0) и образующей с осью Оу угол в 60°.
Задача №4. Через точку А (3;-4;6) провести прямую, параллельную биссектрисе координатного угла yOz.
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Написать уравнение прямой, проходящей че­рез точку 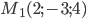$M_{1}(2;-3;4)$ и перпендикулярной прямым

$$\frac{x+2}{1}=\frac{y-3}{-1}=\frac{z+1}{1};\; \frac{x+4}{2}=\frac{y-0}{1}=\frac{z-4}{3}$$

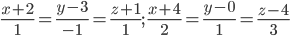
Задача №6.Найти уравнения перпендикуляра, общего к двум прямым

$$\frac{x+2}{1}=\frac{y-3}{-1}=\frac{z+1}{1};\; \frac{x+4}{2}=\frac{y-0}{1}=\frac{z-4}{3}$$

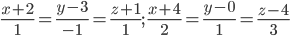
Решения задач №5 и №6 подробно изложены в следующем видео

Задача №7.. Составить уравнение плоскости, проходящей через точку 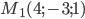$M_{1}(4;-3;1)$ и параллельно прямым

$$\frac{x-0}{6}=\frac{y-0}{2}=\frac{z-0}{-3};\; \frac{x+1}{5}=\frac{y-3}{4}=\frac{z-4}{2}.$$

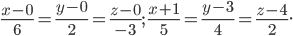
Задача №8. Составить уравнение плоскости, проходящей через прямую

$$\left\{\begin{matrix} x-y+3=0,\\ 6y+1=0 \end{matrix}\right.$$

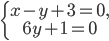
и пересекающей другую прямую

$$\frac{x-1}{1}=\frac{y}{1}=\frac{z+1}{4}$$

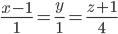
под углом 45°.
Решения задач №7 и №8 подробно изложены в следующем видео

Задача №9. Найти проекцию точки A(1;-3;2) на плос­кость

$$6x+3y-z-41=0.$$

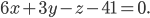
Задача №10. Составить канонические уравнения прямой, лежащей в плоскости xOz, проходящей через начало координат и перпендикулярную к прямой

$$\frac{x-2}{3}=\frac{y+1}{-2}=\frac{z-5}{1}.$$

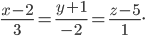
Решения задач №9 и №10 подробно изложены в следующем видео