Пример 9. Исключите иррациональность из знаменателя:
а) 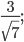 б)
б) 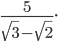
Решение.
а) 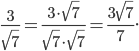
б) 
Ответ: а) 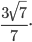 б)
б) 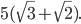
Пример 10. Найдите значение выражения 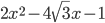 , если
, если 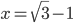 .
.
Решение.
Подставляя в заданное выражение значение  , получим
, получим 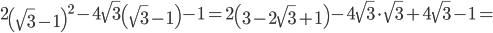
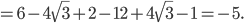
Ответ: 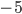 .
.
Пример 11. При каких значениях а имеет смысл выражение 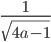 ?
?
Решение.
Учитывая, что квадратный корень определён на множестве неотрицательных чисел, а знаменатель дроби отличен от нуля, выражение 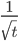 имеет смысл при . Значит, выражение
имеет смысл при . Значит, выражение 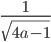 имеет смысл, если . Отсюда
имеет смысл, если . Отсюда
Ответ: 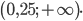
Пример 12. Найдите наименьшее целое число, входящее в область допустимых значений выражения 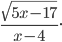
Решение.
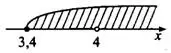
ОДЗ: 
Следовательно, наименьшим целым числом, входящим в область допустимых значений исходного выражения, является 5.
Ответ: 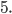
Рациональным называется число, которое можно представить в виде 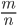 , где
, где 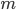 — целое,
— целое,  — натуральное. Например,
— натуральное. Например, 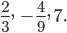 Остальные числа называют иррациональными.
Остальные числа называют иррациональными.
Если — несократимая дробь (и числитель, и знаменатель нельзя сократить на одно и то же число), то 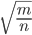 иррационально.
иррационально.
Сумма рациональных чисел рациональна. Целое число называется чётным, если оно делится на 2, и нечётным в противном случае.
Пример 13. Какое из указанных чисел является рациональным?
1) 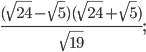
2) 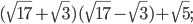
3) 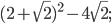
4) 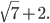
Решение.
Преобразуем каждое выражение:
1) 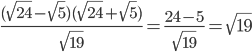 - иррациональное число;
- иррациональное число;
2) 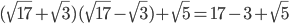 — иррациональное число;
— иррациональное число;
3) 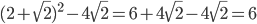 — рациональное число;
— рациональное число;
4) 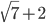 — иррациональное число.
— иррациональное число.
Ответ: 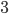 .
.







