Общее кратное нескольких чисел. Наименьшее общее кратное (НОК). Математика 6 класс. Урок №5
Выпишем числа, кратные 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, С, 33, 36, ...
и числа, кратные 4: 8, 12, 16, 20, 24, 28, 32, 36, ...
Общими кратными чисел 3 и 4 будут 12,24, 36, .... наименьшее из которых 12. Это число называют наименьшим общим кратным чисел 3 и 4.
Наименьшим общим кратным двух натуральных чисел называется наименьшее натуральное число, которое делится на каждое из данных чисел. Наименьшее общее кратное двух чисел  и
и  обозначают так: НОК (
обозначают так: НОК ( ). Следовательно, можно записать, что НOК (3, 4) = 12.
). Следовательно, можно записать, что НOК (3, 4) = 12.
Для того, чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложения других чисел;
4) найти произведение полученных множителей.
Если одно из данных чисел делится на все другие числа, тогда это число и является наименьшим общим кратным данных чисел.
Полный урок смотрите в следующем видео:
Домашнее задание:
1. Найди наименьшее общее кратное чисел:
а) 48 и 60; б) 396 и 180; в) 168,231, 60;
г) 280 и 70; д) 80 и 120; е) 250, 125, 370; ё) 3180, 2120, 5300.
2. Найди наименьшее общее кратное чисел  и
и 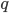 , если
, если  ;
;  .
.
3. В порту начинаются три туристических пароходных рейсов, первый из которых длится 15 суток, второй - 20 суток и третий - 12 суток. Вернувшись в порт, пароходы этот же день снова идут в рейс. Сегодня из порта вышли пароходы по всем трем маршрутам. Через сколько дней они впервые снова вместе пойдут в плавание?







