Общий делитель нескольких чисел. Наибольший общий делитель. Математика 6 класс. Урок №4
Выпишем все делители числа 45: 1; 3; 5; 9; 15; 45 и все делители числа 30: 1; 2; 3, 5, 6; 10, 15; 30. Общие делители: 1; 3; 5; 15. Самый большой из них - 15.
Наибольшим общим делителем двух натуральных чисел называется наибольшее натуральное число, на которое делится каждое из данных чисел.
Наибольший общий делитель двух чисел  и
и  обозначают так: НОД (
обозначают так: НОД ( ). Поэтому можно записать так: НОД (30; 45) = 15.
). Поэтому можно записать так: НОД (30; 45) = 15.
Для того, чтобы найти НОД (36; 54), надо числа 36 и 54 разложить на простые множители и подчеркнуть все те множители, которые являются общими в обоих разложения - 2,3, 3. Произведение общих множителей дает ответ: НОД (36; 54) = 2·3·3 = 18.
Для того, чтобы найти наибольший общий делитель двух чисел, надо:
1) разложить данные числа на простые множители;
2) найти (подчеркнуть) все совместные простые множители в полученных разложениях;
3) найти произведение общих простых множителей.
По этому же правилу можно найти наибольший общий делитель для трех и более чисел.
Если данные числа не имеют общих простых множителей, тогда общим делителем этих чисел будет число 1.
Натуральные числа, наибольший общий делитель которых равен 1, называют взаимно простыми числами.
Если одно натуральное число делится на второе, тогда меньше число и является наибольшим общим делителем данных чисел.
Полный урок смотрите в следующем видео:
Домашнее задание:
1. Найди наибольший общий делитель чисел:
а) 16 и 32; б) 11,22 и 55; в) 500 и 400;
г) 30 и 60; д) 7920 и 594; е) 320, 640, 960; ё) 22, 88, 60.
2. Какое наибольшее число одинаковых комплектов можно составить из елочных игрушек, если есть: 8 снежинок, 24 колокольчиков, 16 шишек, 48 шариков? По сколько каждых игрушек будет в каждом комплекте?
3. Найди наибольший общий делитель чисел  и
и 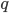 , если
, если  и
и  .
.
4. Докажи, что числа 481 и 555 не является взаимно простыми.
5. Какое наибольшее число одинаковых подарков можно составить из 320 орехов, 240 конфет и 200 пряников? Сколько конфет, орехов и пряников будет в каждом пакете?
6. Из цифр 3, 5, 6 составь все возможные трехзначные числа, в которых все цифры разные. Найди наибольший общий делитель этих чисел.
7. Дети получили на новогоднем празднике одинаковые подарки. Во всех подарках вместе было 128 апельсинов и 82 яблока. Сколько детей присутствовало на празднике? Сколько апельсинов и сколько яблок было в каждом подарке?







