Система двух уравнений с двумя переменными называется однородной, если левые части ее уравнений, содержащие переменные, есть однородные многочлены степени n от двух переменных. Таким образом, однородная система с двумя переменными имеет вид
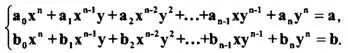
Однородные системы решаются с помощью применения методов алгебраического сложения и введения новых переменных.
Пример 1. Решить систему
![]()
Решение. Левые части обеих уравнений системы — однородные многочлены второй степени от переменных х и у. Если в первом уравнении системы положить х = 0, то получим
2 · 0² + 0 · у - у² = 0 <=> у² = 0 <=> у = 0.
Однако пара (0;0), являющаяся решением первого уравнения системы, не удовлетворяет второму уравнению, т. к. 0²-3·0·0 + 0² = 0 ≠-1. Отсюда х ≠0, и поэтому можем обе части первого уравнения системы разделить на х² ≠ 0 (это не приведет к потере корней). Разделив обе части первого уравнения системы
на х², получим
![]()
Сделав замену
![]()
получим t² -1 - 2 = 0 <=> t₁ =2, t₂ =-1.
Тогда
![]()
или
![]()
Таким образом, исходная система равносильна совокупности двух систем уравнений:
![]()
Первая из этих систем имеет два решения: х₁ =1, у₁ = 2; х₂ = —1; у₂ = -2.
Вторая система несовместна. Отсюда (1;2), (—1;—2) - решения исходной системы.
Ответ: (1;2); (—1;—2).
Пример 2. Решить систему
![]()
Решение. Умножим первое уравнение на 13 и сложим со вторым уравнением
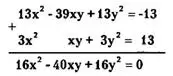
Разделив обе части полученного уравнения на 8, имеем 2х²-5ху + 2у² =0. Таким образом, получаем следующую систему уравнений, равносильную исходной:
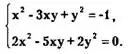
Второе уравнение последней системы можем разделить на х² ≠ 0 (х ≠ 0, так как если положить х = 0, то получим у = 0, а пара (0;0) не удовлетворяет первому уравнению последней системы).
![]()
Положив y/x = t, получаем 2t ²- 5t + 2 = 0 <=> t₁ = 2, t₂ = 1/2.
Тогда y/x=2 <=> y=2x или y/x=1/2 <=> x=2y.
Поэтому исходная система равносильна совокупности систем:
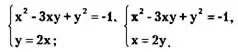
Первая система имеет решения (1;2),(-1;-2); вторая система - (2;1),(-2;-1).
Ответ: {(1;2),(-1;-2); (2;1),(-2;-1)}.
Однородные системы уравнений







