Системы уравнений: общие понятия и основные методы решения

Несколько уравнений с двумя (или более) переменными образуют систему уравнений, если ставится задача найти множество общих решений этих уравнений. Систему двух уравнений с двумя переменными обозначают фигурными скобками и обычно записывают в виде

Множество упорядоченных пар, троек (в случае систем с тремя переменными) и т. д. значений переменных, обращающих в истинное равенство каждое уравнение системы, называется решением системы уравнений.
Решить систему уравнений — значит найти все ее решения или доказать, что решений нет. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Система уравнений называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесчисленное множество решений.
Две системы называются равносильными, если они имеют одно и то же множество решений.
Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными. Если система из n линейных уравнений содержит n неизвестных, то возможны следующие три случая:
1) система не имеет решений;
2) система имеет ровно одно решение;
3) система имеет бесконечно много решений.
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных. Так, для системы двух линейных уравнений с двумя неизвестными

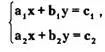
имеем:
а) если

то система имеет единственное решение; геометрически это решение иллюстрируется как точка пересечения двух прямых, являющихся графиками уравнений системы;
б) если

то система не имеет решений; в этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают;
в) если

то система имеет бесконечное множество решений; в этом случае прямые совпадают.
ОСНОВНЫМИ МЕТОДАМИ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ ЯВЛЯЮТСЯ СЛЕДУЮЩИЕ:
1) метод подстановки;
2) метод алгебраического сложения (или метод преобразования системы);
3) метод замены переменных.
При решении системы методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую. Полученное выражение подставляют в другое уравнение системы, в результате чего приходят к уравнению с одной переменной, затем решают это уравнение и находят соответствующее значение второй переменной.
При решении системы методом алгебраического сложения переходят от данной системы к равносильной ей системе, в которой одно из уравнений содержит только одну переменную. При этом обычно умножают одно или оба уравнения на числовые множители таким образом, чтобы коэффициенты при х или у были одинаковыми, но с противоположными знаками.
Пример 1. Решить систему уравнений

Решение. Решим исходную систему двумя способами: методом подстановки и методом алгебраического сложения.
1 способ (метод подстановки).

Из уравнения (а)

Подставляя в уравнение (б), получаем

<=> 15х-48 + 8х = -25 <=> 23х = 23 <=> х=1,

Итак, окончательно х=1, у = 2.
2 способ (метод алгебраического сложения). Решая этим способом, умножим первое уравнение системы на 3, а второе на (-2) и сложим:

6х + 15у - 6х + 8у = 36 + 10 <=> 23у = 46 <=>

окончательно х=1, у=2.
Заметим, что решение исходной системы методом подстановки можно было бы оформить следующим образом, используя только равносильные преобразования и символ <=>.


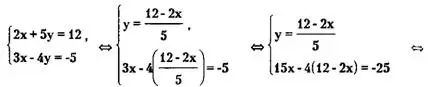
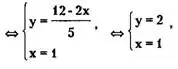
Ответ: {(1;2)}.
Пример 2. Решить систему

Решение. Решаем систему методом подстановки. Из первого уравнения системы у= (7-х), подставив во второе уравнение системы вместо у выражение 7 - х, получаем:

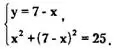
Из второго уравнения системы находим х:
х² + (7 - х)² = 25 <=> х² + 49 - 14х + х² = 25 <=>
2х² - 14х + 24 = 0 <=> х² - 7х +12 = 0 => x₁ = 3, х₂ = 4.
Поэтому данная система имеет два решения:

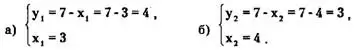
Таким образом, x₁ =3, y₁ = 4; х₂ = 4, у₂ = 3.
Заметим, что решение исходной системы с использованием только равносильных преобразований и совокупности систем можно оформить следующим образом:


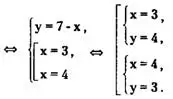
Ответ: {(3;4);(4;3)}.
Пример 3. Решить систему

Решение, х³ + у³ =(х + у)(х²-ху + у²) . Поскольку х²-ху + у²=3 (это первое уравнение исходной системы), то (х + у)³ = 9<=> х + у = 3. Таким образом, мы получили уравнение первой степени (линейное уравнение), которое совместно с первым уравнением исходной системы определяет новую систему:


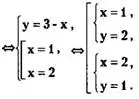
Ответ: {(1;2), (2;1)}.
Пример 4. Решить систему

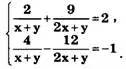
Решение. Решаем систему уравнений методом замены переменных. Положив

приходим к системе уравнений:

Умножив первое уравнение последней системы на (-2) и сложив со вторым уравнением, получим

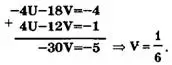
Тогда

Следовательно, имеем систему уравнений, равносильную исходной:

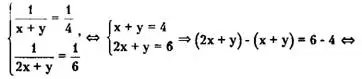
х = 2, у = 4-х = 4-2 = 2 .
Ответ: {(2;2)}.
Пример 5. Решить систему

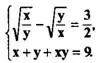
Решение. ОДЗ:

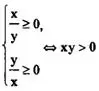
<=>х и у — оба положительные или оба отрицательные.
В первом уравнении системы положим

Тогда

<=> 2t² -3t-2 = 0<=>t₁=2, t₂=-1/2.
Поскольку t>0 => t₂=-1/2 является посторонним корнем.

Таким образом, получаем систему, равносильную исходной:

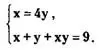
Подставив х = 4у во второе уравнение последней системы, получаем
4у + у + 4у·у = 9<=>4у² + 5у-9 = 0 <=> у₁ = 1, у₂ =-9/4 => x₂=4y₂=4·(-9/4)=-9.
Ответ: {(4;1), (-9;-9/4)}