Нахождение значений тригонометрических функций. Часть 2

Пример 5. Упростить 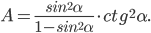$A=\frac{sin^{2}\alpha }{1-sin^{2}\alpha }\cdot ctg^{2}\alpha .$
Решение.

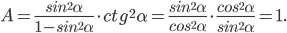
$A=\frac{sin^{2}\alpha }{1-sin^{2}\alpha }\cdot ctg^{2}\alpha =\frac{sin^{2}\alpha}{cos^{2}\alpha }\cdot \frac{cos^{2}\alpha }{sin^{2}\alpha}=1.$

Ответ:

$A=1$ .
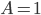Пример 6. Упростить

$A=(sin\alpha -cos\alpha )^{2}+(cos\alpha +sin\alpha )^{2}-2.$
Решение.

$A=(sin\alpha -cos\alpha )^{2}+(cos\alpha +sin\alpha )^{2}-2=$

$=sin^{2}\alpha -2sin\alpha cos\alpha +cos^{2}\alpha +cos^{2}\alpha +2sin\alpha cos\alpha +sin^{2}\alpha-2=$

$=2(sin^{2}\alpha +cos^{2}\alpha )-2=2\cdot 1-2=0.$
Ответ:

$A=0$ .
Пример 7. Упростить

$A=\sqrt{1-sin^{2}\frac{\alpha }{2} }+\sqrt{1-cos^{2}\frac{\alpha }{2} }$ , если

$3\pi <\alpha <4\pi .$
Решение.

$A=\sqrt{1-sin^{2}\frac{\alpha }{2} }+\sqrt{1-cos^{2}\frac{\alpha }{2}}=\sqrt{cos^{2}\frac{\alpha }{2} }+\sqrt{sin^{2}\frac{\alpha }{2}}=\left | cos \frac{\alpha }{2}\right |+\left | sin\frac{\alpha }{2} \right |.$
Избавимся от модулей.

$3\pi <\alpha <4\pi\Rightarrow \frac{3\pi }{2}<\frac{\alpha }{2}<\frac{4\pi }{2}$ следовательно угол

$\frac{\alpha }{2}$ оканчивается в IV четверти отсюда

$\left | cos\frac{\alpha }{2} \right |=cos\frac{\alpha }{2},\; \left | sin\frac{\alpha }{2} \right |=-sin\frac{\alpha }{2}.$

Значит

$A=cos\frac{\alpha }{2}-sin\frac{\alpha }{2}.$ Ответ:

$A=cos\frac{\alpha }{2}-sin\frac{\alpha }{2}.$
Пример 8. Дано

$sin\alpha +cos\alpha =m$ .
Найти: a)

$sin\alpha \cdot cos\alpha$ ; 6)

$sin^{3}\alpha + cos^{3}\alpha$ .
Решение.
а) Возведем обе части исходного выражения в квадрат:

$sin\alpha + cos\alpha=m\Rightarrow (sin\alpha + cos\alpha)^{2}=m^{2}\Leftrightarrow sin^{2}\alpha +2sin\alpha cos\alpha +cos^{2}\alpha =m^{2}\Leftrightarrow$

$\Leftrightarrow 1+2sin\alpha cos\alpha=m^{2}\Leftrightarrow 2sin\alpha cos\alpha=m^{2}-1\Leftrightarrow sin\alpha cos\alpha=\frac{m^{2}-1}{2}.$
б)

$sin^{3}\alpha + cos^{3}\alpha=(sin\alpha +cos\alpha )(sin^{2}\alpha -sin\alpha cos\alpha +cos^{2}\alpha )=$

$=(sin\alpha +cos\alpha )(1-sin\alpha cos\alpha )=m\left ( 1-\frac{m^{2}-1}{2} \right )=m\left ( \frac{2-m^{2}+1}{2} \right )=\frac{m(3-m^{2})}{2}.$
В процессе решения мы учли, что если

$sin\alpha +cos\alpha =m$ , то