Для периодической функции 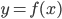 выполняется равенство
выполняется равенство 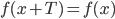 , где
, где 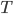 — отличное от нуля число, называемое периодом функции. Каждая периодическая функция имеет бесчисленное множество периодов, т. к. если
— отличное от нуля число, называемое периодом функции. Каждая периодическая функция имеет бесчисленное множество периодов, т. к. если 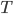 — период, то
— период, то 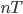 — период, где
— период, где 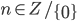 . Обычно, говоря о периоде, имеют в виду наименьший положительный период, который называется основным. Основными периодами для тригонометрических функций являются:
. Обычно, говоря о периоде, имеют в виду наименьший положительный период, который называется основным. Основными периодами для тригонометрических функций являются: 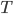 = 360° для функций
= 360° для функций 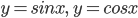 ;
; 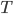 = 180° для функций
= 180° для функций 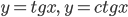 . В более общем виде можем записать:
. В более общем виде можем записать:
 ,
,

Если углы выражать в радианах, то можно сказать, что периоды функций 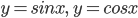
 , а периоды функций
, а периоды функций 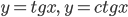
 .
.
При этом  — основной период функций
— основной период функций 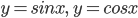 ;
;  — основной период функций
— основной период функций 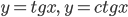 .
.
Известно, что периоды функций  и
и  вычисляются по формуле
вычисляются по формуле  , а периоды функций
, а периоды функций  и
и  — по формуле
— по формуле  .
.
Если период функции 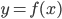 равен
равен  а период функции
а период функции  равен
равен  , то период функций
, то период функций  и
и  равен наименьшему числу, при делении которого на
равен наименьшему числу, при делении которого на  и
и  получаются целые числа.
получаются целые числа.
Пример 1. Вычислить без использования калькулятора и таблиц: a)  ; б)
; б)  ; в)
; в)  .
.
Решение.
а) 
б) 
в) 
Ответ: a)  ; б)
; б)  ; в)
; в)  .
.
Пример 2. Найти период функций: а)  ; б)
; б)  ; в)
; в)  .
.
Решение.
а) Период функции  равен
равен  , а период функции
, а период функции  равен
равен  . Наименьшее число, при делении которого на
. Наименьшее число, при делении которого на  и
и  — получаются целые числа, есть число
— получаются целые числа, есть число 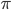 . Следовательно, период заданной функции равен
. Следовательно, период заданной функции равен  .
.
б) Находим периоды слагаемых. Период функции  равен
равен  , а период функции
, а период функции  равен
равен  . Очевидно, что период заданной функции равен
. Очевидно, что период заданной функции равен  .
.
в) Период функции  равен
равен  , а период функции
, а период функции  равен
равен  . Периода у заданной функции не существует, т. к. нет такого числа, при делении которого на 2 и на
. Периода у заданной функции не существует, т. к. нет такого числа, при делении которого на 2 и на 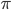 одновременно получались бы целые числа.
одновременно получались бы целые числа.
Ответ: а)  ; б)
; б)  ; в) периода
; в) периода 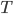 не существует.
не существует.
Периодичность тригонометрических функций






