Четность и нечетность тригонометрических функций
При повороте единичного вектора 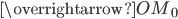 (начального радиуса
(начального радиуса 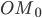 на углы
на углы  и
и 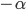 абсциссы векторов
абсциссы векторов 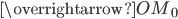 и
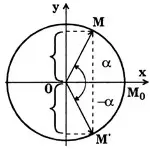
и 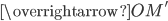 равны, а ординаты равны по модулю, но противоположны по знаку (рис. 1). Это значит, что
равны, а ординаты равны по модулю, но противоположны по знаку (рис. 1). Это значит, что 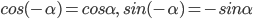 , т.е. функция
, т.е. функция 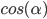 является четной, a
является четной, a 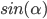 — нечетной.
— нечетной.
Рассмотрим остальные тригонометрические функции:

Отсюда  . Следовательно, функция
. Следовательно, функция  является нечетной.
является нечетной.

Отсюда  Следовательно, функция
Следовательно, функция  является нечетной.
является нечетной.
Таким образом, из четырех основных тригонометрических функций функция  является четной, а остальные три — нечетными.
является четной, а остальные три — нечетными.
Пример 1. Исследовать на четность функции:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  .
.
Решение.
а)  Следовательно, функция
Следовательно, функция  является нечетной;
является нечетной;
б)  Следовательно, функция
Следовательно, функция  является четной;
является четной;
в)  Следовательно, функция
Следовательно, функция  является нечетной;
является нечетной;
г)  Следовательно, функция
Следовательно, функция  является нечетной;
является нечетной;
д)  Следовательно, функция
Следовательно, функция  не является ни четной, ни нечетной, т. е. это функция общего вида.
не является ни четной, ни нечетной, т. е. это функция общего вида.






