Помимо тождества 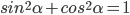 , основными тригонометрическими тождествами называются также следующие соотношения:
, основными тригонометрическими тождествами называются также следующие соотношения:
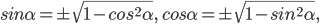
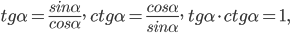
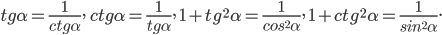
В формулах
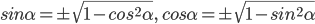 знаки "+" или "-" выбираются в зависимости от того, в какой четверти оканчивается угол
знаки "+" или "-" выбираются в зависимости от того, в какой четверти оканчивается угол  . Так, если
. Так, если  оканчивается в I или II четверти, то берем знак "+", а если в III или IV четверти, то знак "-" в формуле
оканчивается в I или II четверти, то берем знак "+", а если в III или IV четверти, то знак "-" в формуле 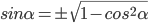 . В формуле
. В формуле 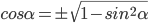 для углов, оканчивающихся в I или IV четвертях, нужно взять знак "+", а если углы оканчиваются во II или III четвертях, то знак "-".
для углов, оканчивающихся в I или IV четвертях, нужно взять знак "+", а если углы оканчиваются во II или III четвертях, то знак "-".





