Рассмотрим вначале тригонометрические функции острого угла, которые можно ввести с помощью прямоугольного треугольника (рис. 1).
Пусть в прямоугольном треугольнике 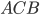 :
:
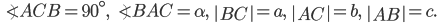
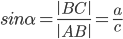 (отношение противолежащего катета к гипотенузе).
(отношение противолежащего катета к гипотенузе).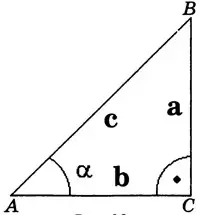
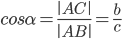 (отношение прилежащего катета к гипотенузе).
(отношение прилежащего катета к гипотенузе).
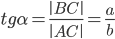 (отношение противолежащего катета к прилежащему).
(отношение противолежащего катета к прилежащему).
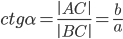 (отношение прилежащего катета к противолежащему).
(отношение прилежащего катета к противолежащему).
Из последних двух равенств следует, что 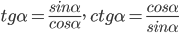 .
.
Рассмотрим тригонометрические функции произвольных значений аргумента.
Имеем прямоугольную систему координат хОу на плоскости и круг единичного радиуса, имеющий центр в начале координат (рис. 2). Такой круг называется единичным кругом или тригонометрическим кругом.
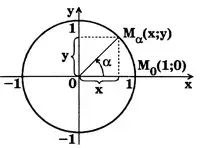
Отметим на оси Ох справа от начала координат точку  , лежащую на тригонометрическом круге:
, лежащую на тригонометрическом круге:  . Радиус
. Радиус  называется начальным радиусом. При повороте начального радиуса
называется начальным радиусом. При повороте начального радиуса 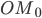 около центра O на угол
около центра O на угол  точка
точка 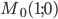 переходит в некоторую точку
переходит в некоторую точку 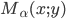 .
.
Синусом угла  называется отношение ординаты точки
называется отношение ординаты точки 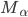 к радиусу.
к радиусу.
Косинусом угла  называется отношение абсциссы точки
называется отношение абсциссы точки 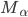 к радиусу.
к радиусу.
Таким образом, 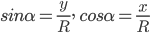 . Поскольку R=l, то
. Поскольку R=l, то 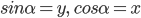 . x и y можно рассматривать как проекции на оси координат единичного вектора
. x и y можно рассматривать как проекции на оси координат единичного вектора 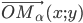 . Таким образом, можно утверждать, что синус угла а равен ординате, а косинус — абсциссе вектора единичной длины, исходящего из начала координат и образующего с положительным направлением оси Ох угол
. Таким образом, можно утверждать, что синус угла а равен ординате, а косинус — абсциссе вектора единичной длины, исходящего из начала координат и образующего с положительным направлением оси Ох угол  . Так как координаты любой точки
. Так как координаты любой точки 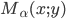 единичной окружности удовлетворяют уравнению
единичной окружности удовлетворяют уравнению 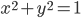 , то
, то 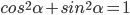 . Соотношение
. Соотношение 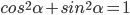 называется основным тригонометрическим тождеством.
называется основным тригонометрическим тождеством.
Тангенсом угла  называется отношение ординаты точки
называется отношение ординаты точки 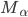 к ее абсциссе:
к ее абсциссе:
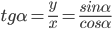 .
.
Котангенсом угла  называется отношение абсциссы точки
называется отношение абсциссы точки 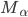 к ее ординате:
к ее ординате:
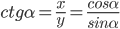 .
.
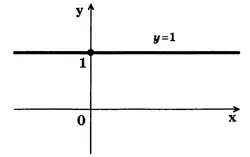
Прямая 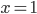 (рис. 3) называется осью тангенсов.
(рис. 3) называется осью тангенсов.
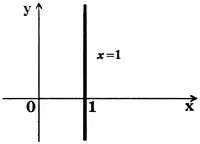
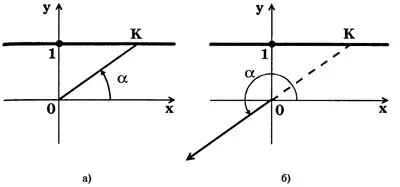
Каждому углу  можно поставить в соответствие точку Т на оси тангенсов, являющуюся точкой пересечения конечной стороны угла
можно поставить в соответствие точку Т на оси тангенсов, являющуюся точкой пересечения конечной стороны угла  (или ее продолжения) с осью тангенсов (рис. 4).
(или ее продолжения) с осью тангенсов (рис. 4).
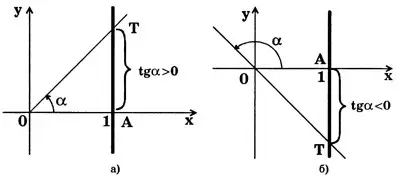
Тангенс угла  равен ординате соответствующей точки Т на оси тангенсов.
равен ординате соответствующей точки Т на оси тангенсов.
Прямая 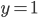 (рис. 5) называется осью котангенсов.
(рис. 5) называется осью котангенсов.
Каждому углу 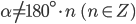 можно поставить в соответствие точку
можно поставить в соответствие точку  на оси котангенсов, являющуюся точкой пересечения конечной стороны угла (или ее продолжения) с осью котангенсов (рис. 6).
на оси котангенсов, являющуюся точкой пересечения конечной стороны угла (или ее продолжения) с осью котангенсов (рис. 6).
Котангенс угла  равен абсциссе соответствующей точки
равен абсциссе соответствующей точки 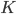 на оси котангенсов.
на оси котангенсов.
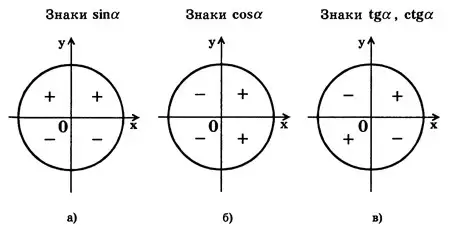
Знаки тригонометрических функций 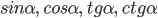 в различных четвертях (квадрантах) даны на рис. 7.
в различных четвертях (квадрантах) даны на рис. 7.
Приведем таблицу значений тригонометрических функций некоторых углов, которые наиболее часто используются на практике (табл. 1).
Таблица 1
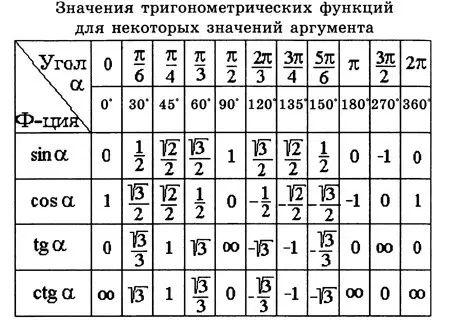
Символ 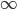 (бесконечность) означает, что
(бесконечность) означает, что 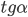 или
или 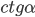 при соответствующих значениях аргумента не определены и принимают сколь угодно большие значения по модулю.
при соответствующих значениях аргумента не определены и принимают сколь угодно большие значения по модулю.
Секансом угла  (обозначение
(обозначение  ) называется величина, обратная
) называется величина, обратная  , т. е.
, т. е. 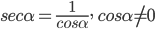 .
.
Косекансом угла  (обозначение
(обозначение  ) называется величина, обратная
) называется величина, обратная 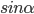 , т.е.
, т.е. 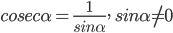 .
.






