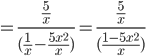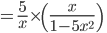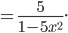Least Common Denominator
The least common denominator (LCD) of two or more fractions is the least
common multiple (LCM) of their denominators. To find the LCD:
1. Factor each denominator completely and write as the product of prime factors.
(Factor trees are usually used for this.)
2. Take the greatest power of each prime factor.
3. Find the product of these factors.
E X A M P L E :
Find the LCD of 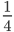 and
and 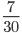 .
.
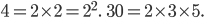
The greatest power of 2 is 2². The greatest power of 3 is 3, and the greatest
power of 5 is 5.
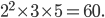
60 is the LCD. (Answer)
The least common denominator is helpful when adding and subtracting
fractions.
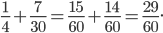
The least common denominator is also used when simplifying complex
fractions. A complex fraction is a fraction whose numerator or denominator
contains one or more fractions. Find the LCD of the simple fractions
and multiply the numerator and denominator of the complex
fraction by it.
E X A M P L E :
Simplify 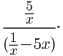
We first start by finding a common denominator for the expression in the
numerator, which is x. This gives us: