Fractions. Multiplying Fractions

Multiplying Fractions

To multiply fractions, simply multiply straight across.

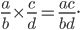
E X A M P L E :
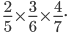
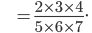
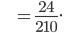Simplify $\displaystyle \; \frac{2}{5}\times \frac{3}{6}\times \frac{4}{7}.\;$
$\displaystyle \;\;\; \; \;\; \; \; =\frac{2\times 3\times 4}{5\times 6\times 7}.\;$
$\displaystyle \;\;\; \; \;\; \; \; =\frac{24}{210}.\;$ Divide by a common factor to simplify.
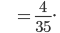$\displaystyle \;\;\; \; \;\; \; \; =\frac{4}{35}.\;$ (Answer)
You can also simplify the fractions before multiplying to save time.
E X A M P L E :
$\displaystyle \frac{2}{5}\times \frac{3}{6}\times \frac{4}{7}=\frac{1}{5}\times \frac{1}{1}\times \frac{4}{7}.$ Remove the common factors of 2 and 3.
$\displaystyle \; \, \; \; \, \; \, \;\; \; \;\; \; \; =\frac{1\times 1\times 4}{5\times 1\times 7}.$
$\displaystyle \; \, \; \; \, \; \, \;\; \; \;\; \; \; =\frac{4}{35}.$
To divide by a fraction, multiply by its reciprocal.
$\displaystyle \; \frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}.$
This is known as the Division Rule for Fractions. Of course, b, c, and d cannot equal zero because you cannot divide by zero.
E X A M P L E :
Simplify $\displaystyle 18\div \frac{6}{11}.$
$\displaystyle =18\times \frac{11}{6}.$
$\displaystyle =3\times \frac{11}{1}. \;$ Divide through by a common factor of 6.
$\displaystyle =\frac{3\times 11}{1}=33.\;$ (Answer)