Задача 1. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведённым в одну из вершин n-угольника (принадлежащих этой стороне), равен 67,5° (см. рис. 1). Найдите n.
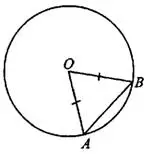
Решение.
Пусть  — сторона n-угольника.
— сторона n-угольника.  — равнобедренный, так как
— равнобедренный, так как  как радиусы, значит, углы при основании равны и
как радиусы, значит, углы при основании равны и  . Найдём
. Найдём 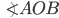 .
.  , откуда
, откуда  Если n-угольник правильный, то
Если n-угольник правильный, то  , тогда
, тогда 
Ответ: 8.
Задача 2. Четырёхугольник 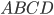 вписан в окружность. Угол
вписан в окружность. Угол  равен 113°, угол
равен 113°, угол  равен 52°. Найдите угол
равен 52°. Найдите угол  . Ответ дайте в градусах (см. рис. 2).
. Ответ дайте в градусах (см. рис. 2).
Решение.
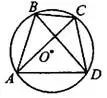
 (как вписанные углы, которые опираются на одну и ту же дугу).
(как вписанные углы, которые опираются на одну и ту же дугу). 
Ответ: 61.
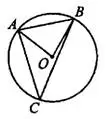
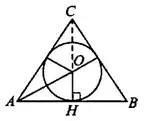
Задача 3. Сторона  остроугольного треугольника ABC равна радиусу описанной около него окружности (см. рис. 3). Найдите угол
остроугольного треугольника ABC равна радиусу описанной около него окружности (см. рис. 3). Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.
Пусть  — центр описанной окружности, тогда по условию
— центр описанной окружности, тогда по условию  и
и  правильный,
правильный,  — центральный угол, который опирается на дугу
— центральный угол, который опирается на дугу  .
.  — вписанный, опирается на дугу
— вписанный, опирается на дугу  .
. 
Ответ: 30.
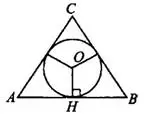
Задача 4. Боковые стороны равнобедренного треугольника равны 25, основание равно 30. Найдите радиус вписанной окружности (см. рис. 4).
Решение.
В равнобедренном треугольнике центр вписанной окружности  лежит на высоте, проведённой к основанию, т.е.
лежит на высоте, проведённой к основанию, т.е.  (см. рис. 5).
(см. рис. 5).  — точка пересечения биссектрис.
— точка пересечения биссектрис.  — биссектриса, она делит сторону
— биссектриса, она делит сторону 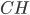 треугольника
треугольника 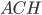 на отрезки, пропорциональные прилежащим сторонам,
на отрезки, пропорциональные прилежащим сторонам, 
 — медиана, как высота, проведённая к основанию равнобедренного треугольника
— медиана, как высота, проведённая к основанию равнобедренного треугольника  ,
,  Из
Из  по теореме Пифагора
по теореме Пифагора

Ответ: 7,5.
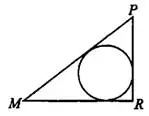
Задача 5. В треугольнике 
 , угол
, угол  равен 90°. Найдите радиус вписанной окружности (см. рис. 6).
равен 90°. Найдите радиус вписанной окружности (см. рис. 6).
Решение.
Воспользуемся формулой для радиуса 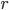 вписанной в прямоугольный треугольник окружности. Пусть
вписанной в прямоугольный треугольник окружности. Пусть  — катеты, а
— катеты, а  — гипотенуза. Тогда
— гипотенуза. Тогда  . Найдём
. Найдём 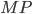 .
.

Ответ: 8.
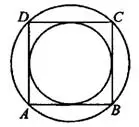
Задача 6. Около окружности, радиус которой равен  , описан квадрат (см. рис. 7). Найдите радиус окружности, описанной около этого квадрата.
, описан квадрат (см. рис. 7). Найдите радиус окружности, описанной около этого квадрата.
Решение.
Если окружность вписана в квадрат, то её диаметр равен стороне квадрата. 
Если окружность описана вокруг квадрата, то её диаметр является диагональю квадрата, радиус равен половине диаметра.  (например, можно получить это из теоремы Пифагора).
(например, можно получить это из теоремы Пифагора).  Тогда
Тогда 
Ответ: 14.







