• Пусть дана бесконечная числовая последовательность  . Если выполняется равенство
. Если выполняется равенство  для всех натуральных
для всех натуральных  и
и  , то такая последовательность называется геометрической прогрессией.
, то такая последовательность называется геометрической прогрессией.
• Число  называют знаменателем геометрической прогрессии.
называют знаменателем геометрической прогрессии.
Например, последовательность чисел 1,3,9,27,81,... является геометрической прогрессией. Знаменатель прогрессии  .
.
•  — формула
— формула  -го члена геометрической прогрессии.
-го члена геометрической прогрессии.
Задача 1. Дана геометрическая прогрессия 2, 6, 18,... . Найдите знаменатель прогрессии.
Решение.

Ответ: 3.
Задача 2. Найдите пятый член геометрической прогрессии, если 
Решение.
По формуле  найдём
найдём

Ответ: 8.
Задача 3. Запишите пять первых членов геометрической прогрессии, если заданы  и
и 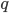 .
.
а) 
б) 
в) 
г) 
Решение.
а) Если  , то
, то

б) Если  , то
, то

в) Если  , то
, то

г) Если  , то
, то

Ответ: а) 4, 8,16, 32,64;
б) -4, -8, -16, -32, -64;
в) 4, -8,16, -32,64;
г) -4, 8,-16, 32, —64.
Задача 3. Найдите пятый член геометрической прогрессии, если 
Решение.
Так как  , то
, то

Ответ: 27.
Геометрическая прогрессия. Готовимся к ОГЭ по математике. Модуль 1. Урок 34







