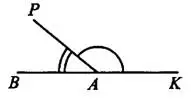
Рассмотрим развёрнутый угол 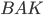 (см. рис. 1). Луч
(см. рис. 1). Луч 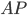 делит его на два смежных угла. Оказывается, синусы этих смежных углов равны, а косинусы противоположны (то есть отличаются только знаком).
делит его на два смежных угла. Оказывается, синусы этих смежных углов равны, а косинусы противоположны (то есть отличаются только знаком).
Например, если 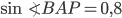 , то
, то 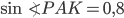 ,
, 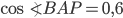 и
и 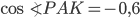 . Тангенсы смежных углов также противоположны.
. Тангенсы смежных углов также противоположны.
Задача 1. В треугольнике  угол
угол  равен 90°,
равен 90°, 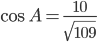 .
.
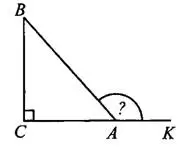
Найдите тангенс внешнего угла при вершине  .
.
Решение.
Внешним углом треугольника называют угол, образованный стороной этого треугольника и продолжением другой его стороны. На рисунке 2 внешний угол при вершине  — это угол
— это угол 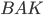 .
.
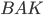 и
и 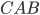 — смежные углы. Тангенсы смежных углов — противоположные числа (отличаются только знаком), поэтому найдём тангенс угла
— смежные углы. Тангенсы смежных углов — противоположные числа (отличаются только знаком), поэтому найдём тангенс угла 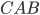 . Тангенсом угла называют отношение противолежащего катета к прилежащему.
. Тангенсом угла называют отношение противолежащего катета к прилежащему.
Для нашего треугольника 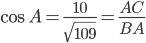 .
.
Будем считать, что 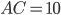 ,
, 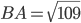 . Найдём
. Найдём 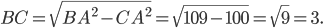 Тогда
Тогда 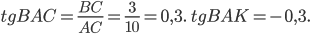
Ответ: -0,3.
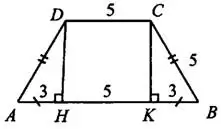
Задача 2. Основания равнобедренной трапеции (см. рис. 3) равны 5 и 11. Боковые стороны равны 5. Найдите синус острого угла трапеции.
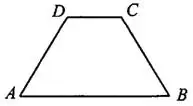
Решение.
В равнобедренной трапеции углы при основании равны. Если опустить высоты из вершин  и
и  на основание
на основание  , то получатся два равных прямоугольных треугольника
, то получатся два равных прямоугольных треугольника  и
и 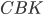 (см. рис. 4).
(см. рис. 4).
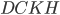 — прямоугольник,
— прямоугольник, 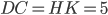 .
. 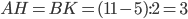 . Синус острого угла трапеции, например
. Синус острого угла трапеции, например  , найдём из прямоугольного треугольника
, найдём из прямоугольного треугольника  . По теореме Пифагора,
. По теореме Пифагора, 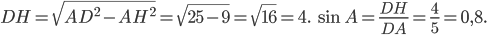
Ответ: 0,8.







