Равнобедренным треугольником называют треугольник, у которого две равные стороны. Эти стороны называют боковыми сторонами, третью сторону называют основанием. Если в задаче дан равнобедренный треугольник, то пользуются его свойствами.
1. В равнобедренном треугольнике углы при основании равны.
2. Высота, проведённая к основанию равнобедренного треугольника (между равными сторонами), является медианой и биссектрисой.
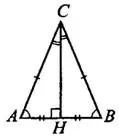
Посмотрим на рисунок 1. В треугольнике  основание
основание  , боковые стороны
, боковые стороны 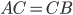 , угол
, угол  равен углу
равен углу  , высота
, высота 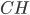 делит
делит  на равные отрезки
на равные отрезки 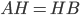 и угол
и угол  на два равных угла.
на два равных угла.
Задача 1. В треугольнике 
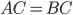 ,
, 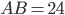 ,
, 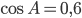 . Найдите высоту
. Найдите высоту 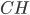 .
.
Решение.
В треугольнике  стороны
стороны 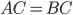 , значит, он равнобедренный. Высота
, значит, он равнобедренный. Высота 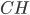 , проведённая к основанию равнобедренного треугольника, делит
, проведённая к основанию равнобедренного треугольника, делит  пополам, поэтому
пополам, поэтому 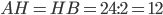 . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник 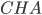 с прямым углом
с прямым углом 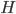 и катетами
и катетами 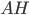 и
и 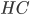 .
. 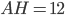 ,
, 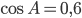 . Найдём
. Найдём 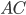 . Косинусом угла называют отношение прилежащего катета к гипотенузе.
. Косинусом угла называют отношение прилежащего катета к гипотенузе.
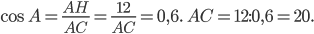
По теореме Пифагора
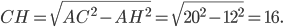
Ответ: 16.
Задача 2. В треугольнике 
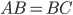 , высота
, высота 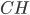 равна 6,
равна 6, 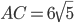 (см. рис. 2). Найдите тангенс угла
(см. рис. 2). Найдите тангенс угла 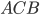 .
.
Решение.
В равнобедренном треугольнике углы при основании равны. В данном треугольнике 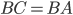 , основание
, основание 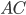 , равны углы
, равны углы 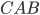 и
и 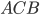 . Следовательно, можно вместо тангенса угла
. Следовательно, можно вместо тангенса угла 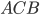 найти тангенс угла
найти тангенс угла 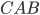 . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник 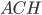 с гипотенузой
с гипотенузой 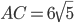 и катетами
и катетами 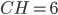 и
и 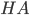 . Длину катета
. Длину катета 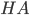 можно найти по теореме Пифагора.
можно найти по теореме Пифагора.
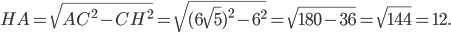
Тангенсом угла называют отношение противолежащего катета к прилежащему. Для нашего треугольника
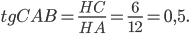
Ответ: 0,5.
Задача 3. В треугольнике 
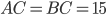 ,
, 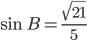 . Найдите
. Найдите  .
.
Решение.
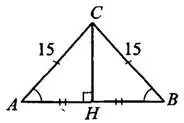
В равнобедренном треугольнике  высота
высота 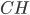 является медианой, значит,
является медианой, значит, 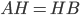 (см. рис. 3). Рассмотрим прямоугольный треугольник
(см. рис. 3). Рассмотрим прямоугольный треугольник 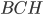 с гипотенузой
с гипотенузой 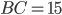 и катетами
и катетами 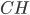 и
и 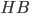 . В данном треугольнике
. В данном треугольнике
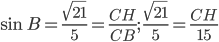 , тогда
, тогда 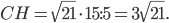
Катет 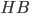 ) можно найти по теореме Пифагора:
) можно найти по теореме Пифагора: 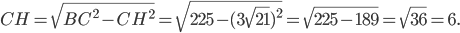
 в два раза больше
в два раза больше 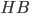 ,
, 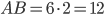 .
.
Ответ: 12.
Задача 4. В треугольнике 
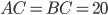 ,
, 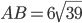 . Найдите
. Найдите 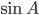 .
.
Решение.
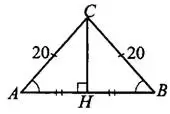
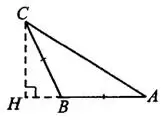
Проведём высоту 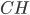 , тогда
, тогда 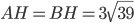 . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник 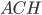 (см. рис. 4). Катет
(см. рис. 4). Катет 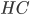 можно найти по теореме Пифагора.
можно найти по теореме Пифагора. 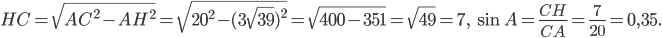
Ответ: 0,35.







