Окружность, касательные и секущие. Готовимся к ЕГЭ по математике. Геометрия. Урок 13

Окружность — это множество точек плоскости, расположенных на одинаковом расстоянии от данной точки (центра).
Отрезок, соединяющий центр окружности с любой точкой окружности, называется радиусом.
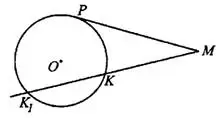
Прямая, имеющая с окружностью только одну общую точку, называется касательной, к — касательная (см. рис. 1).

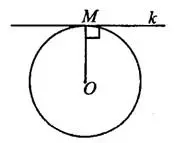
Прямая, имеющая с окружностью две общие точки, называется секущей.
Свойства касательных и секущих.
1°. Касательная перпендикулярна радиусу, проведённому в точку касания.
2°. Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через центр окружности и эту общую точку.
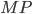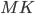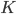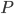Пусть дана окружность с центром $O$, $MP$ и $MK$ — касательные, $K$ и $P$ — точки касания, следовательно 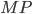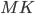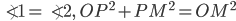$MP$ = $MK$, $\displaystyle \angle 1=\angle 2,\; OP^{2}+PM^{2}=OM^{2}$ (см. рис. 2).

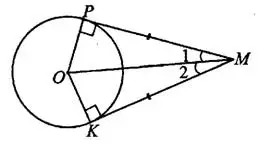
3°. Если касательная пересекается с секущей, то квадрат отрезка касательной равен произведению расстояний от общей точки прямых до точек пересечения секущей с окружностью.
Пусть дана окружность с центром 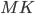$O$, $MK$ — секущая, 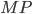$MP$ — касательная, 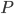$P$ — точка касания, следовательно, 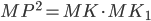$\displaystyle MP^{2}=MK\cdot MK_{1}$ (см. рис. 3).

Хорда — это отрезок, концы которого лежат на окружности.

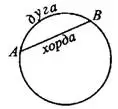
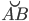$AB$ — хорда, $\displaystyle \breve{AB}$ — дуга (см. рис. 4).
Дуга — это часть окружности, соединяющая две точки окружности (см. рис. 4).
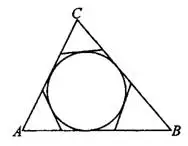
Задача 1. К окружности, вписанной в треугольник $ABC$, проведены три касательные (см. рис. 5). Периметры отсечённых треугольников равны 5, 6, 8. Найдите периметр треугольника $ABC$.

Решение.
Рассмотрим рис. 6. Периметр 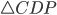$\displaystyle \bigtriangleup CDP$ равен $\displaystyle DC+CP+PM+MD$, также $\displaystyle P_{BGE}=BG+GF+FE+EB,\; P_{ANR}=NA+AR+RL+LN.$

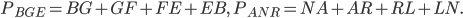
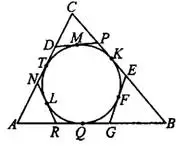
Но отрезки 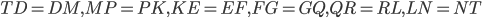$TD = DM, MP = PK, KE = EF, FG = GQ, QR = RL, LN = NT$ как отрезки касательных к окружности, проведённых из одной точки. Тогда
$\displaystyle P_{ABC}=AB+BC+CA=P_{CDP}+P_{BGE}+P_{ANR}=5+6+8=19.$
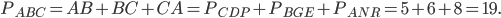
Ответ: 19.