• Допустимые значения переменных — это значения, при которых алгебраическое выражение имеет смысл.
• Если в выражении есть дробь, то знаменатель дроби должен быть отличен от нуля.
Например, для выражения 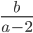 допустимыми являются значения переменных, удовлетворяющие условию
допустимыми являются значения переменных, удовлетворяющие условию 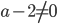 , то есть
, то есть 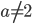 .
.
• Если в алгебраическом выражении есть квадратный корень, то подкоренное выражение должно быть неотрицательно.
Например, для выражения 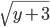 допустимыми являются значения переменных, удовлетворяющие условию
допустимыми являются значения переменных, удовлетворяющие условию 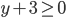 , то есть
, то есть 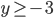 .
.
Пример 1. Найдите допустимые значения переменной  в выражении
в выражении 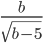
Решение.
Выражение под корнем должно быть неотрицательным, поэтому 6 — 5^0, 6^5. Кроме того, знаменатель должен быть отличен от нуля, поэтому 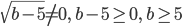 . Таким образом, одновременно должно выполняться
. Таким образом, одновременно должно выполняться 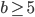 и
и 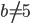 , следовательно, .
, следовательно, .
Ответ: .
Пример 2. Найдите количество целых чисел, входящих в область допустимых значении переменной  в выражении
в выражении 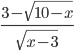 .
.
Решение. 1-й способ.
В числителе под корнем стоит выражение 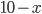 , поэтому
, поэтому 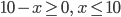 . В знаменателе под корнем стоит выражение
. В знаменателе под корнем стоит выражение 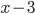 , поэтому
, поэтому 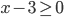 . Кроме того, знаменатель должен быть отличен от нуля, поэтому последнее неравенство должно быть строгим: . Мы нашли область допустимых значений:
. Кроме того, знаменатель должен быть отличен от нуля, поэтому последнее неравенство должно быть строгим: . Мы нашли область допустимых значений: 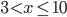 . В неё входят целые числа 4, 5, 6, 7, 8, 9, 10 — всего 7 чисел.
. В неё входят целые числа 4, 5, 6, 7, 8, 9, 10 — всего 7 чисел.
2-й способ.
Покажем запись решения, если рассуждения выполнять устно.
Неравенство 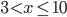 имеет 7 целых решений: 4, 5, 6, 7, 8, 9, 10.
имеет 7 целых решений: 4, 5, 6, 7, 8, 9, 10.
Ответ: 7.







