Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:

Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:
частота =кратность варианты/объём измерения
В нашем примере частота варианты «4» равна  .
.
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен  .
.
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное  .
.
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию:  .
.
2. Если объём измерения нечётный, то есть  , то получим следующую ситуацию:
, то получим следующую ситуацию:
![]()
В этом случае медианой является число  .
.
3. Если объём измерения чётный, то есть  , то имеем
, то имеем
![]()
В этом случае медианой является число —  .
.
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно 
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
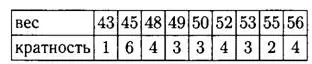
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
Продолжая аналогично, заполним таблицу:
б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант: 
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен 
Ответ: 13.
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.
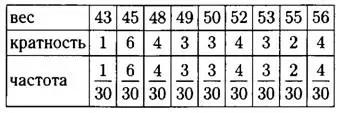
д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.
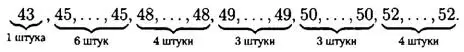
Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна 
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
 .
.
Осталось разделить полученную сумму на количество всех чисел:  .
.
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда:  , размах:
, размах:  . Искомое значение равно
. Искомое значение равно  .
.
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна  , процентная частота равна
, процентная частота равна  .
.
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно  , но в этой группе нет половины котов, удовлетворяющих требованиям.
, но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна  . То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет
. То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет  бракованных.
бракованных.
Ответ: 6010.







