Теория вероятностей. Готовимся к ОГЭ по математике. Модуль 3. Урок 64

Случайным называют событие, которое может произойти или не произойти (заранее предсказать невозможно) во время наблюдения или испытания.
Пусть при проведении испытания (бросание монеты или кубика, вытягивание экзаменационного билета и т.д.) всегда наступает один из $n$ равновозможных исходов. Например, при подбрасывании монеты число всех исходов $n$ равно 2, так как кроме выпадения «решки» или «орла», других исходов быть не может. При броске игрального кубика возможны 6 исходов, так как на верхней грани кубика равновозможно появление любого из чисел от 1 до 6. 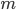Пусть также некоторому событию $A$ благоприятствуют $m$ исходов.
Вероятностью события $A$ называется отношение числа благоприятных для этого события исходов к общему числу равновозможных исходов. Пишем $\displaystyle P(A)=\frac{m}{n}$.
Например, пусть событие $A$ состоит в выпадении нечётного числа очков при броске кубика. Всего возможны 6 исходов: выпадение на верхней грани кубика 1, 2, 3, 4, 5, 6. При этом благоприятными для события $A$ являются исходы с выпадением 1, 3, 5. Таким образом, $\displaystyle P(A)=\frac{3}{6}=0,5$.
Заметим, что всегда выполняется двойное неравенство $0\leq m\leq n$, поэтому вероятность любого события $A$ лежит на отрезке [0; 1], то есть $0\leq P(A)\leq 1$.
Задача 1. Из 1000 собранных на заводе телевизоров 5 штук бракованные. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найдите вероятность того, что проверяемый телевизор окажется бракованным.
Решение.
При выборе телевизора наугад возможны 1000 исходов; событию $A$ «выбранный телевизор бракованный» благоприятны 5 исходов. По определению вероятности
$\displaystyle P(A)=\frac{5}{1000}=0,005$.
Ответ: 0,005.
Задача 2. В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
Решение.
Общее число исходов равно числу шаров: $9+6+5=20$.
Число исходов, благоприятствующих данному событию, равно 6. Искомая вероятность равна $\displaystyle \frac{6}{20}=0,3$.
Ответ: 0,3.

События $A$ и $B$ называются противоположными друг другу, если любой исход благоприятен ровно для одного из них. Например, в рассмотренной задаче №1 событие «выбранный телевизор рабочий» является противоположным событию «выбранный телевизор бракованный».
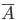Событие, противоположное событию $A$, обозначают $\bar{A}$. Из определения противоположных событий следует $P(A)+P(\bar{A})=1$, значит $P(\bar{A})=1-P(A)$.
Задача 1. Из 30 билетов, предлагаемых на экзамене, школьник может ответить только на 27. Какова вероятность того, что школьник не сможет ответить на наугад выбранный билет?
1-й способ.
Обозначим через $A$ событие «школьник может ответить на билет». Тогда $\displaystyle P(A)=\frac{27}{30}=0,9$. Вероятность противоположного события равна $P(\bar{A})=1-P(A)=1-0,9=0,1$.
2-й способ.
Так как школьник может ответить на 27 билетов, то на 3 билета он ответить не может. Вероятность получить один из этих билетов равна $\displaystyle \frac{3}{30}=0,1$.
Ответ: 0,1.