Векторы
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется вектором.
Точка плоскости называется нулевым вектором.
Длиной или модулем вектора 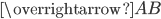 называется длина отрезка
называется длина отрезка  . Длина вектора обозначается
. Длина вектора обозначается  .
.
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарные векторы бывают сонаправленными ( ↑↑
↑↑  ) (см. рис.1) и противоположно направленными (
) (см. рис.1) и противоположно направленными ( ↓↓
↓↓  ) (см. рис.2).
) (см. рис.2).

Рис.1 Рис.2
Сумма и разность векторов
1. 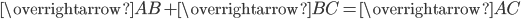 ;
;
2.  ;
;
3. 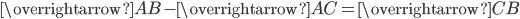 .
.
На рисунке 3 показано, как построить сумму и разность векторов  и
и  .
.
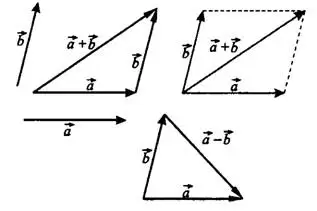
Рис.3
4. Умножение вектора на число.
 — такой вектор, длина которого равна
— такой вектор, длина которого равна  и который при сонаправлен с
и который при сонаправлен с  , при
, при  противоположно направлен
противоположно направлен  (см. рис.4).
(см. рис.4).
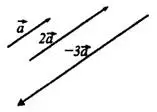
Рис.4
5. Если  — середина
— середина  , то
, то  .
.
Скалярное произведение векторов и его свойства
 , где
, где  — угол между векторами
— угол между векторами  и
и  (см. рис.5)
(см. рис.5)


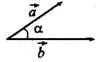
Рис.5



Координаты вектора
Чтобы найти координаты вектора, нужно из координат конца вектора вычесть координаты начала. Если точки  и
и  заданы координатами
заданы координатами  и
и  , то координаты вектора
, то координаты вектора
 .
.
Длина отрезка  .
.
Например, на рисунке 6 координаты точек  . Координаты вектора
. Координаты вектора  , то есть
, то есть  .
.  .
.
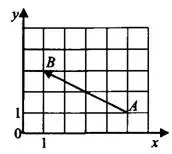
Рис.6
Координаты середины отрезка следует находить по формулам

Например, на рисунке 6 координаты середины отрезка  равны
равны 
Если  , то
, то
1. вектор 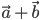 имеет координаты
имеет координаты  ;
;
2. вектор 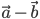 имеет координаты
имеет координаты  ;
;
3. вектор  имеет координаты
имеет координаты  ;
;
4. 
5.  .
.
Задача 1. Найдите координаты векторов  , если известно, что
, если известно, что  .
.
Решение.



Ответ: {-3; -5}, {7; -1}, {10; -15}.
Задача 2. Найдите скалярное произведение векторов  и
и  .
.
Решение.

Ответ: 18.
Задача 3. Длина вектора  равна 4, длина вектора
равна 4, длина вектора  равна 10, а длина вектора
равна 10, а длина вектора 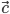 равна 5. Найдите
равна 5. Найдите  и
и  , если известно, что угол между векторами
, если известно, что угол между векторами  и
и  равен 120°, а векторы
равен 120°, а векторы  и
и 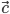 сонаправлены.
сонаправлены.
Решение.

Тогда 
По условию,  ↑↑
↑↑  значит, между ними угол 0°, то есть
значит, между ними угол 0°, то есть  .
.
Ответ: -20; 20.
Задача 4. Длина вектора  равна 12, длина вектора
равна 12, длина вектора  равна 5. Найдите длину вектора
равна 5. Найдите длину вектора  , если вектор
, если вектор  перпендикулярен вектору
перпендикулярен вектору  .
.
Решение.
Построим рисунок 7.
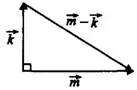
Рис.7
 , поэтому
, поэтому  можно найти как гипотенузу прямоугольного треугольника с катетами 5 и 12.
можно найти как гипотенузу прямоугольного треугольника с катетами 5 и 12. 
Ответ: 13.
Задача 5. Найдите отрицательную координату  если расстояние от точки
если расстояние от точки  до точки
до точки  равно 5.
равно 5.
Решение.
Запишем расстояние от  до
до 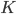 :
:  .
.
Тогда 

Выберем отрицательную координату  .
.
Ответ: -7.







