Площадь треугольника (задачи на клетчатой бумаге). Готовимся к егэ по математике. Геометрия. Урок 2

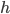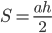
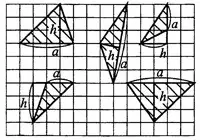
Площадь произвольного треугольника равна половине произведения длины его стороны ($a$) на высоту ($h$), проведённую к этой стороне: $\displaystyle S=\frac{ah}{2}$
На рисунке 1 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон $a$ и высота, проведённая к этой стороне $h$.
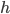Как правило, удобно брать ту сторону, которая проходит по линиям клетчатой бумаги (или же проходит параллельно осям координат).

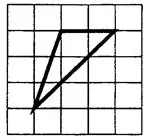
Задача 1. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треугольник (см. рис. 2). Найдите его площадь в квадратных сантиметрах.
Решение.
1-й способ.

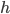Площадь произвольного треугольника равна половине произведения длины его стороны ($a$) на высоту ($h$), проведённую к этой стороне. Проведём высоту 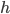$h$. Треугольник тупоугольный, поэтому высота проводится вне треугольника.

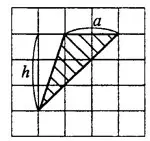
На рисунке 3 сторона $a$ = 2 см, высота $h$ = 3 см.
$\displaystyle S=\frac{ah}{2}=\frac{2\cdot 3}{2}=3$ см².
Ответ: 3.
Заметим, что так как клетки имеют размер 1 см х 1 см, то площадь в квадратных сантиметрах получится, если мы будем по рисунку считать размер отрезков в клетках. Поэтому единицы длины в этих задачах можно и не писать.
2-й способ.
Достроим треугольник $BCM$ до прямоугольного треугольника $MCA$ (см. рис. 4).

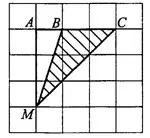
Тогда искомую площадь треугольника $BCM$ можно найти как разность площадей двух прямоугольных треугольников $MAC$ и $MAB$.
Катеты первого из них равны 3 см и 3 см, катеты второго — Зсм и 1 см.
Площадь прямоугольного треугольника равна половине произведения его катетов, следовательно,
$\displaystyle S_{MAC}=\frac{3\cdot 3}{2}=4,5;\; S_{MAB}=\frac{1\cdot 3}{2}=1,5;$
$\displaystyle S_{MBC}=S_{MAC}-S_{MAB}=4,5-1,5=3.$
Ответ: 3.