Рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных на клетчатой бумаге или расположенных на координатной плоскости.
Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.
 ) равен сумме квадратов катетов (
) равен сумме квадратов катетов ( и
и  ):
): 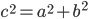 .
.
Площадь прямоугольного треугольника равна половине произведения его катетов:
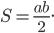
Напомним, что у прямоугольного треугольника есть прямой угол, равный 90°. Сторона напротив прямого угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.
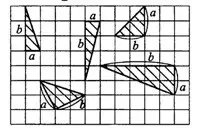
На рисунке 1 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты  и
и  .
.
Задача 1. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треугольник (см. рис. 2). Найдите его площадь в квадратных сантиметрах.
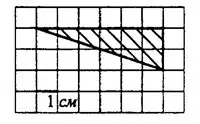
Решение.
Площадь прямоугольного треугольника равна половине произведения его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем по клеточкам), поэтому площадь
 (см²)
(см²)
Ответ: 6.
Теперь рассмотрим задачу, в которой точки изображены на координатной плоскости. Напомним, что любая точка на координатной плоскости характеризуется двумя числами — координатами. Первая координата называется абсциссой ( ), вторая координата называется ординатой (
), вторая координата называется ординатой ( ). На рисунке 3 точки A, B и C имеют координаты A(4; 10), B(0; 2), C(8; 2).
). На рисунке 3 точки A, B и C имеют координаты A(4; 10), B(0; 2), C(8; 2).
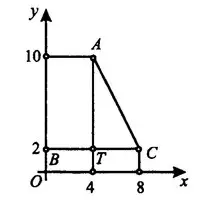
Посмотрим внимательно на рисунок 3. Если у двух точек одинаковые абсциссы ( ), как у точек
), как у точек 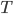 и
и  , или одинаковые ординаты (
, или одинаковые ординаты ( ), как у точек В, Т и С, то соответствующие отрезки параллельны осям координат.
), как у точек В, Т и С, то соответствующие отрезки параллельны осям координат.  параллелен
параллелен  ,
, 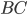 параллелен
параллелен  . В таких случаях длину отрезка легко найти, если вычесть различающиеся координаты точек.
. В таких случаях длину отрезка легко найти, если вычесть различающиеся координаты точек.
Например, найдём длину отрезка AT, где А{4; 10), Т(4; 2). Абсциссы (х) у них равны. Найдём разность ординат (у), длина  равна 10 - 2 = 8.
равна 10 - 2 = 8.
Длину отрезка  , параллельного оси
, параллельного оси  , можно найти, если вычесть их абсциссы: 8 — 4 = 4.
, можно найти, если вычесть их абсциссы: 8 — 4 = 4.
Длину 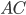 найдём по теореме Пифагора. Треугольник
найдём по теореме Пифагора. Треугольник  прямоугольный,
прямоугольный,  .
. 
Задача 2. Найдите площадь треугольника (в см²), вершины которого имеют координаты (4; 2), (6; 2), (4; 10) (см. рис. 4).
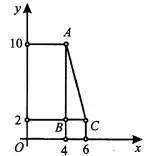
Решение. 1-й способ.
Площадь прямоугольного треугольника равна половине произведения его катетов. Найдём длину катета 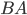 . Абсциссы (
. Абсциссы ( ) у них равны. Находим разность ординат (
) у них равны. Находим разность ординат ( ), длина АВ равна 10 — 2 = 8. Длину отрезка
), длина АВ равна 10 — 2 = 8. Длину отрезка 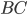 , параллельного оси
, параллельного оси  , можно найти, если вычесть их абсциссы: 6 — 4 = 2. Тогда площадь
, можно найти, если вычесть их абсциссы: 6 — 4 = 2. Тогда площадь  (см²).
(см²).
Ответ: 8.
2-й способ.
Нанесём координатную сетку (нарисуем линии с промежутком 1 прямо на данном чертеже, рис. 5).
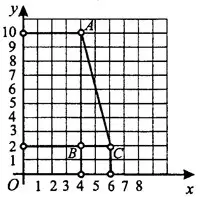
После этого по клеточкам посчитаем длину катетов и вычислим площадь.  = 8,
= 8, 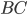 = 2,
= 2,  (см²).
(см²).
Ответ: 8.
При этом способе решения задач важно не ошибиться и не пропускать числа и линии в координатной сетке, их нужно проводить с разницей в единицу.







