Координаты вектора. Готовимся к ЕГЭ по математике. Геометрия. Урок 10

Пусть точки $A$ и $B$ имеют координаты $\displaystyle A(x_{A};y_{A}),\; B(x_{B};y_{B})$.
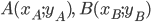Координаты вектора 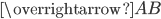$\displaystyle \overrightarrow{AB}$ вычисляются по формуле
$\displaystyle x=x_{B}-x_{A},\; y=y_{B}-y_{A}.$
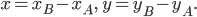
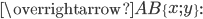
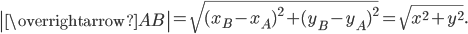
Длина вектора, или модуль вектора $\displaystyle \overrightarrow{AB}\left \{ x;y \right \}:$
$\displaystyle \left | \overrightarrow{AB} \right |=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}=\sqrt{x^{2}+y^{2}}.$
Заметим, что если ввести координатные векторы $i$ и $j$ так, что длины этих векторов равны 1, а направление вектора $\displaystyle \vec{i}$ совпадает с направлением оси $Ox$, вектора $\displaystyle \vec{j}$ — оси $Oy$, то любой вектор $\displaystyle \vec{a}$ на координатной плоскости можно представить в виде разложения $\displaystyle \vec{a}=x\vec{i}+y\vec{j}$, где числа $x$, $y$ называют координатами вектора $\displaystyle \vec{a}$. Обычно записывают $\displaystyle \vec{a}\left \{ x;y \right \}$ или $\displaystyle \vec{a}(x;y)$.
Координаты суммы и разности векторов $\displaystyle \vec{a}\left \{ x_{a};y_{a} \right \}$ и $\displaystyle \vec{b}\left \{ x_{b};y_{b} \right \}$:
$\displaystyle \vec{a}+\vec{b}=\vec{c}\left \{ x_{c};y_{c} \right \},\; x_{c}=x_{a}+x_{b},\; y_{c}=y_{a}+y_{b}.$
$\displaystyle \vec{a}-\vec{b}=\vec{p}\left \{ x_{p};y_{p} \right \},\; x_{p}=x_{a}-x_{b},\; y_{p}=y_{a}-y_{b}.$
Для параллелограмма известно, что его противоположные стороны равны и параллельны. Например, для параллелограмма 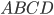$ABCD$ (см. рис. 1) $\displaystyle \overrightarrow{AB}=\overrightarrow{DC}$, так как $AB = CD$ и $AB$ || $CD$.

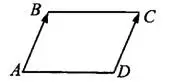
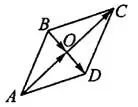
Диагонали параллелограмма пересекаются в середине диагоналей, поэтому $\displaystyle \overrightarrow{AO}=\overrightarrow{OC}$, $\displaystyle \overrightarrow{BO}=\overrightarrow{OD}$ (см. рис. 2).

Скалярное произведение векторов $\displaystyle \vec{a}\cdot \vec{b}=\left | \vec{a} \right |\cdot \left | \vec{b} \right |\cdot cos\alpha$, где $\displaystyle \alpha$ — угол между векторами $\displaystyle \vec{a}$ и $\displaystyle \vec{b}$.
Если векторы заданы координатами $\displaystyle \vec{a}\left \{ x_{a};y_{a} \right \},\; \vec{b}\left \{ x_{b};y_{b} \right \}$, то $\displaystyle \vec{a}\cdot \vec{b}=x_{a}\cdot x_{b}+y_{a}\cdot y_{b}.$
Задача 1. Найдите длину вектора $\displaystyle \vec{a}\left \{ 5;-12 \right \}$ (см. рис. 3).

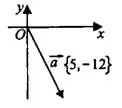
Решение.
$\displaystyle \left | \vec{a} \right |=\sqrt{x^{2}+y^{2}}=\sqrt{5^{3}+(-12)^{2}}=13.$
Ответ: 13.
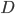Задача 2. Точки $\displaystyle A(-1;-2),\; B(4;-1),\; C(6;5)$ и $D$ являются вершинами параллелограмма. Найдите ординату точки 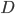$D$ (см. рис. 4).

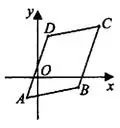
Решение.
Стороны параллелограмма 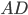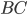$AD$||$BC$ и $AD = BC$, поэтому $\displaystyle \overrightarrow{AD}=\overrightarrow{BC}$. Найдём ординаты векторов $\displaystyle \overrightarrow{AD}$ и $\displaystyle \overrightarrow{BC}$. $\displaystyle y_{D}-y_{A}=y_{C}-y_{B},\; y_{D}-(-2)=5-(-1),\; y_{D}=6-2=4.$
Ответ: 4.
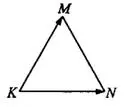
Задача 3. Стороны правильного треугольника $MKN$ равны 10 (см. рис. 5). Найдите скалярное произведение векторов $\displaystyle \overrightarrow{KN}$ и $\displaystyle \overrightarrow{KM}$.

Решение.
Скалярное произведение векторов вычисляют по формуле $\displaystyle \overrightarrow{KN}\cdot \overrightarrow{KM}=\left | \overrightarrow{KN} \right |\cdot \left | \overrightarrow{KM} \right |\cdot cos\alpha$, где $\displaystyle \alpha$ — угол между векторами. В правильном $\displaystyle \bigtriangleup MKN$ углы равны по 60°, поэтому $\displaystyle \overrightarrow{KN}\cdot \overrightarrow{KM}=10\cdot 10\cdot cos60^{\circ}=100\cdot 0,5=50$.
Ответ: 50.
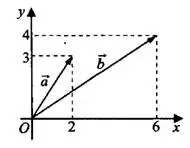
Задача 4. Найдите сумму координат вектора $\displaystyle \vec{a}-\vec{b}$ (см. рис. 6).

Решение.
Найдём координаты вектора $\displaystyle \vec{a}$. Он выходит из начала координат, поэтому его координаты равны координатам его конца: $\displaystyle \vec{a}\left \{ 2;3 \right \}$. Аналогично $\displaystyle \vec{b}\left \{ 6;4 \right \}$.
$\displaystyle \vec{a}-\vec{b}$ имеет координаты {2 — 6; 3 — 4}, то есть {—4; —1}. Сумма координат —4 + (—1) = —5.
Ответ: —5.
Задача 5. Найдите квадрат длины вектора $\displaystyle \vec{a}+\vec{b}$ (см. рис. 6).
Решение.
$\displaystyle \vec{a}\left \{ 2;3 \right \},\; \vec{b}\left \{ 6;4 \right \}$. Тогда $\displaystyle \vec{a}+\vec{b}$ имеет координаты {2 + 6; 3 + 4} или {8; 7}.
$\displaystyle \left | \vec{a}+\vec{b} \right |^{2}=8^{2}+7^{2}=64+49=113.$
Ответ: 113.
Задача 6. Найдите скалярное произведение векторов $\displaystyle \vec{a}$ и $\displaystyle \vec{b}$ (см. рис. 6).
Решение.
$\displaystyle \vec{a}\left \{ 2;3 \right \},\; \vec{b}\left \{ 6;4 \right \}.$ Тогда $\displaystyle \vec{a}\cdot \vec{b}=x_{a}\cdot x_{b}+y_{a}\cdot y_{b}=2\cdot 6+3\cdot 4=24.$
Ответ: 24.
Задача 7. ННайдите угол между векторами а и Ь (см. рис. 7). Ответ выразите в градусах.

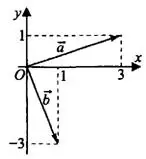
Решение.
$\displaystyle \vec{a}\left \{ 3;1 \right \},\; \vec{b}\left \{ 1;-3 \right \}$.
Тогда $\displaystyle cos\alpha =\frac{\vec{a}\cdot \vec{b}}{\left | \vec{a} \right |\cdot \left | \vec{b} \right |}=\frac{3\cdot 1+1\cdot (-3)}{\left | \vec{a} \right |\cdot \left | \vec{b} \right |}=0.$
$\displaystyle \alpha =90^{\circ}.$
Ответ: 90.