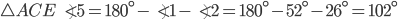Свойства треугольника. Готовимся к ЕГЭ по математике. Геометрия. Урок 11

Сумма длин трёх сторон треугольника называется его периметром.
$\displaystyle P_{\bigtriangleup ABC}=AB+BC+AC$.
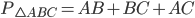Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
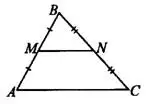
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
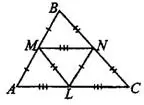
На рисунке 1 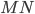$MN$ — средняя линия треугольника $ABC$.

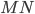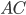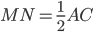1. Средняя линия треугольника параллельна его стороне и равна половине этой стороны. $MN$||$AC$, $\displaystyle MN=\frac{1}{2}AC$.
2. Средние линии треугольника делят его на четыре равных треугольника (см. рис. 2).

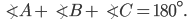
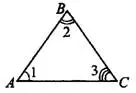
Сумма углов треугольника равна 180°. На рисунке 3 $\displaystyle \angle A+\angle B+\angle C=180^{\circ}.$

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

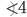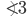Например, $\displaystyle \angle 4$ и $\displaystyle \angle 3$ — смежные, следовательно, 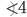$\displaystyle \angle 4$ — внешний угол треугольника ABC (см. рис. 4).
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Угол 4 — внешний угол треугольника $ABC$. $\displaystyle \angle 4=\angle 1+\angle 2.$
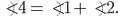
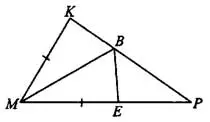
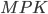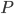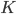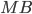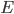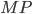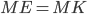Задача 1. В треугольнике $MPK$ угол $P$ равен 35° (см. рис. 5), угол $K$ равен 95°, $MB$ — биссектриса, $E$ — такая точка на $MP$, что $ME = MK$. Найдите угол 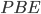$PBE$. Ответ дайте в градусах.

Решение.
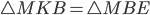$\displaystyle \bigtriangleup MKB=\bigtriangleup MBE$ по первому признаку (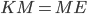$KM = ME$ по условию, 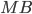$MB$ — общая сторона. 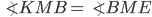$\displaystyle \angle KMB=\angle BME$, так как 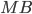$MB$ — биссектриса),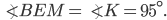 $\displaystyle \angle BEM=\angle K=95^{\circ}.$
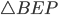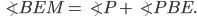
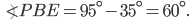
Внешний угол $\displaystyle \bigtriangleup BEP$ равен сумме двух углов треугольника, не смежных с ним, то есть $\displaystyle \angle BEM=\angle P+\angle PBE.$
$\displaystyle \angle PBE=95^{\circ}-35^{\circ}=60^{\circ}.$
Ответ: 60.
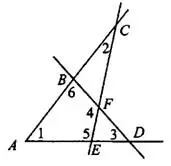
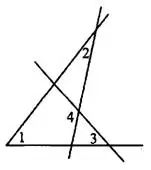
Задача 2. На рисунке 6 угол 1 равен 52°, угол 2 равен 26°, угол 3 равен 48°. Найдите угол 4. Ответ дайте в градусах.
Решение.
Сумма углов треугольника равна 180°, а четырёхугольника — 360°.

В 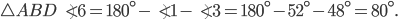$\displaystyle \bigtriangleup ACE\; \angle 5=180^{\circ}-\angle 1-\angle 2=180^{\circ}-52^{\circ}-26^{\circ}=102^{\circ}$ (см. рис. 7).

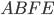
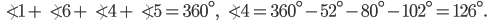
В $\displaystyle \bigtriangleup ABD\; \angle 6=180^{\circ}-\angle 1-\angle 3=180^{\circ}-52^{\circ}-48^{\circ}=80^{\circ}.$ В четырёхугольнике $ABFE$ $\displaystyle \angle 1+\angle 6+\angle 4+\angle 5=360^{\circ},\; \angle 4=360^{\circ}-52^{\circ}-80^{\circ}-102^{\circ}=126^{\circ}.$
Ответ: 126.