Задача 3. В треугольнике 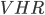 стороны
стороны 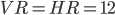 , высота
, высота 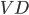 равна 6,(см. рис. 8). Найдите угол
равна 6,(см. рис. 8). Найдите угол 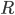 . Ответ дайте в градусах.
. Ответ дайте в градусах.
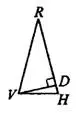
Решение.
В прямоугольном 
 , гипотенуза
, гипотенуза  , катет
, катет  . Если катет равен половине гипотенузы,
. Если катет равен половине гипотенузы,
то напротив этого катета лежит угол, равный 30°. Поэтому  .
.
Ответ: 30.
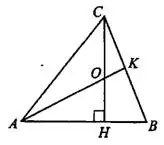
Задача 4. В треугольнике 
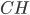 — высота,
— высота,  — биссектриса,
— биссектриса,  — точка пересечения прямых
— точка пересечения прямых 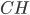 и
и  , угол
, угол 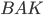 равен 31°. Найдите угол
равен 31°. Найдите угол  . Ответ дайте в градусах (см. рис. 9).
. Ответ дайте в градусах (см. рис. 9).
Решение.
 — биссектриса, значит,
— биссектриса, значит, 
В  Рассмотрим
Рассмотрим  .
.

Ответ: 121.
Задача 5. Острые углы прямоугольного треугольника равны 39° и 51°. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах (см. рис. 10).
Решение.
В 
 — биссектриса,
— биссектриса, 
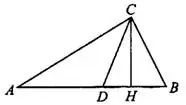
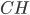 — высота,
— высота,  Нужно найти
Нужно найти  , он равен разности
, он равен разности 
Найдём  из
из  .
. 
Ответ: 6.
Задача 6. Один из внешних углов треугольника равен 85°. Углы, не смежные с данным внешним углом, относятся как 2 : 3 (см. рис. 11). Найдите наибольший из них. Ответ дайте в градусах.
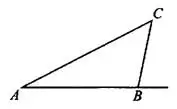
Решение.
Сумма углов, не смежных с данным внешним углом, равна величине этого внешнего угла, то есть  Обозначим
Обозначим 

 — наибольший из углов
— наибольший из углов  и
и  .
.
Ответ: 51.
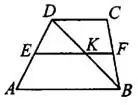
Задача 7. Основания трапеции  и
и  равны 14 и 10 соответственно (см. рис. 12). Найдите больший из отрезков, на которые делит среднюю линию этой трапеции диагональ
равны 14 и 10 соответственно (см. рис. 12). Найдите больший из отрезков, на которые делит среднюю линию этой трапеции диагональ  .
.
Решение.
Средняя линия трапеции параллельна основаниям трапеции, и её концы являются серединами боковых сторон.  Параллельные прямые
Параллельные прямые  и
и  проходят через концы равных отрезков на одной прямой
проходят через концы равных отрезков на одной прямой  , значит, и на прямой
, значит, и на прямой  они отсекают равные отрезки (по теореме Фалеса).
они отсекают равные отрезки (по теореме Фалеса).  и
и  — средние линии
— средние линии  и
и  . Средняя линия треугольника равна половине параллельной ей стороны,
. Средняя линия треугольника равна половине параллельной ей стороны,  Больший из отрезков равен 7.
Больший из отрезков равен 7.
Ответ: 7.
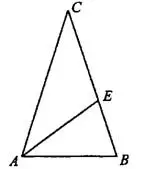
Задача 8. В треугольнике  проведена биссектриса
проведена биссектриса  .
.  Найдите меньший угол треугольника
Найдите меньший угол треугольника  . Ответ дайте в градусах (см. рис. 13).
. Ответ дайте в градусах (см. рис. 13).
Решение.
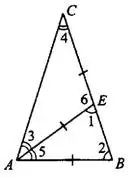
 — равнобедренный, и углы при основании равны (см. рис. 14).
— равнобедренный, и углы при основании равны (см. рис. 14).  . Аналогично в равнобедренном
. Аналогично в равнобедренном
 , так как
, так как  — биссектриса.
— биссектриса.  как суммы углов треугольников. Обозначим
как суммы углов треугольников. Обозначим 


Меньший угол равен 36°.
Ответ: 36.
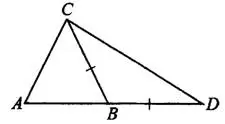
Задача 9. В треугольнике  угол
угол  равен 48°,
равен 48°,  На продолжении стороны
На продолжении стороны  отложен отрезок
отложен отрезок  . Найдите угол
. Найдите угол  . Ответ дайте в градусах (см. рис. 15).
. Ответ дайте в градусах (см. рис. 15).
Решение.
Сумма углов треугольника равна 180°, 
 — равнобедренный (
— равнобедренный ( ), следовательно углы при основании равны,
), следовательно углы при основании равны, 
Ответ: 30.
Задача 10. В треугольнике 
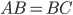 . Внешний угол при вершине
. Внешний угол при вершине  равен 156°. Найдите угол
равен 156°. Найдите угол  . Ответ дайте в градусах (см. рис. 16).
. Ответ дайте в градусах (см. рис. 16).
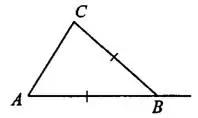
Решение.
Внешний угол треугольника равен сумме углов, не смежных с ним.  — равнобедренный, углы при основании равны.
— равнобедренный, углы при основании равны. 
Ответ: 78.







