При делении десятичной дроби на натуральное число надо
• разделить дробь на это число, не обращая внимания на запятую;
• поставить в частном запятую, когда кончится деление целой части. Если целая часть меньше делителя, то частное начинается с нуля целых.
Упражнение 1. Вычислите: а) 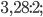 б)
б) 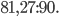
Решение.

Ответ: а) 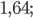 б)
б) 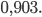
При делении десятичной дроби на 10,100,1000,... надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
При этом иногда необходимо написать перед целой частью нуль или несколько нулей.
Упражнение 2. Выполните деление: а) 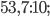 6)
6) 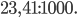
Решение.
а) 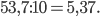
б) 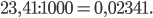
Ответ: а) 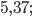 б)
б) 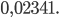
При делении чисел на десятичную дробь надо
• в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
• после этого выполнить деление на натуральное число.
Упражнение 3. Выполните деление: а) 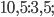 6)
6) 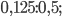 в)
в) 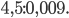
Решение.
а) 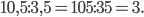
б) 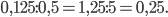
в) 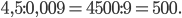
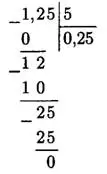
Ответ: а)  б)
б) 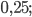 в)
в) 
Упражнение 4. Найдите значение выражения: а) 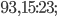 б)
б) 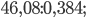 в)
в) 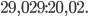
Решение.

Ответ: а) 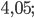 6)
6) 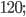 в)
в) 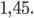
При делении обыкновенных дробей надо делимое умножить на число, обратное делителю. (Два числа, произведение которых равно 1, называют взаимно обратными.)
Упражнение 5. Выполните деление: а) 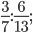 б)
б) 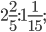 в)
в) 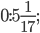 г)
г) 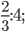 д)
д) 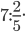
Решение.
а) 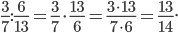
б) 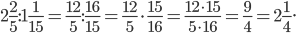
в) 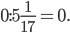
г) 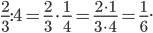
д) 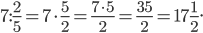
Ответ: а) 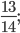 б)
б) 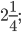 в)
в) 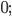 г)
г) 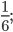 д)
д) 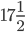 .
.
При делении отрицательного числа на отрицательное надо разделить модуль делимого на модуль делителя.
Упражнение 6. Выполните деление: а) 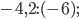 б)
б) 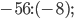 в)
в) 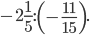
Решение.
а) 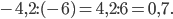
б) 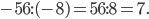
в) 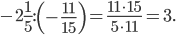
Ответ: а) 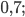 6)
6) 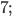 в)
в) 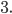
При делении чисел с разными знаками надо
• поставить знак минус;
• разделить модуль делимого на модуль делителя.
Упражнение 7. Выполните деление: а) 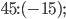 б)
б) 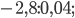 в)
в) 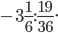
Решение.
а) 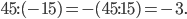
б) 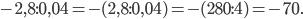
в) 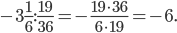
Ответ: а) 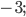 б)
б) 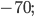 в)
в)