Описанные и вписанные окружности (теория). Готовимся к ЕГЭ по математике. Геометрия. Урок 16

Окружность называют вписанной в угол или многоугольник (в частности, в треугольник), если она касается всех сторон соответствующего угла или многоугольника (см. рис. 1).

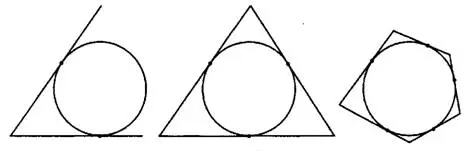
Окружность называют описанной вокруг многоугольника, если все его вершины лежат на этой окружности (см. рис. 2).

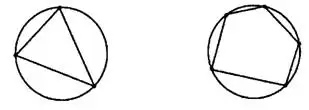
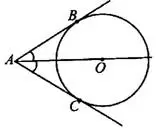
1°. Центр вписанной в угол окружности лежит на биссектрисе угла.
Окружность с центром $O$ вписана в угол $BAC$, следовательно, $\displaystyle \angle BAO=\angle CAO$ (см. рис. 3).
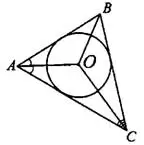
2°. Центр вписанной в многоугольник окружности лежит в точке пересечения его биссектрис.

В $\displaystyle \bigtriangleup ABC$ точка $O$ — центр вписанной окружности, следовательно, $BO, CO, AO$ — биссектрисы углов $\displaystyle \bigtriangleup ABC$ (см. рис. 4).

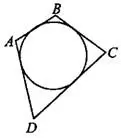
3°. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.
Окружность вписана в четырёхугольник 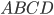$ABCD$, значит $\displaystyle AD+BC=AB+DC$. (см. рис. 5).

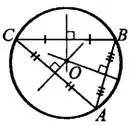
4°. Центр описанной окружности многоугольника — точка пересечения серединных перпендикуляров к его сторонам.
$\displaystyle \bigtriangleup ABC$ вписан в окружность, $O$ — центр (см. рис. 6).

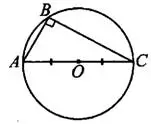
5°. Центр окружности, описанной около прямоугольного треугольника, — середина гипотенузы.
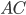$\displaystyle \bigtriangleup ABC$ вписан в окружность с центром $O$, $\displaystyle \angle B=90^{\circ}$, значит $\displaystyle AO=OC$, точка $O$ лежит на $AC$ (см. рис. 7).

6°. Радиус 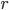$r$ окружности, вписанной в прямоугольный треугольник, можно вычислить по формуле $\displaystyle r=\frac{a+b-c}{2}$ где $a$ и $b$ — катеты, $c$ — гипотенуза.
7°. Центры вписанной и описанной окружности правильного треугольника совпадают, центр лежит на высоте треугольника и делит её в отношении 2:1, считая от вершины.
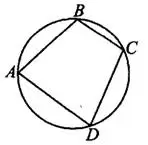
8°. Если четырёхугольник вписан в окружность, суммы его противоположных углов равны 180°.
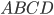$ABCD$ вписан в окружность (см. рис. 8). $\displaystyle \angle A+\angle C=\angle B+\angle D=180^{\circ}.$

9°. Если трапеция вписана в окружность, то она равнобедренная.