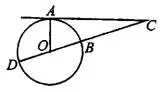
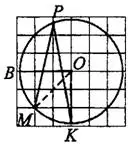
Задача 1. Найдите угол 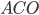 , если прямая
, если прямая 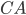 касается окружности в точке
касается окружности в точке  , точка
, точка  — центр окружности, дуга
— центр окружности, дуга 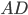 окружности, заключённая внутри этого угла, равна 128° (см. рис. 1). Ответ дайте в градусах.
окружности, заключённая внутри этого угла, равна 128° (см. рис. 1). Ответ дайте в градусах.
Решение.
Угол между касательной и радиусом, проведённым в точку касания, прямой:  . Центральный угол
. Центральный угол  равен угловой величине дуги, на которую он опирается, то есть
равен угловой величине дуги, на которую он опирается, то есть  Внешний угол треугольника равен сумме двух углов, не смежных с ним,
Внешний угол треугольника равен сумме двух углов, не смежных с ним, 
Ответ: 38.
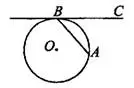
Задача 2. Хорда  стягивает дугу окружности в 104°. Найдите угол
стягивает дугу окружности в 104°. Найдите угол  между этой хордой и касательной к окружности, проведённой через точку
между этой хордой и касательной к окружности, проведённой через точку  . Ответ дайте в градусах (см. рис. 2).
. Ответ дайте в градусах (см. рис. 2).
Решение.
Угол между хордой и касательной к окружности, проведённой из конца хорды, равен половине угловой величины дуги, которую стягивает эта хорда. 
Ответ: 52.
Задача 3. Через концы  и
и  дуги окружности в 56° проведены касательные
дуги окружности в 56° проведены касательные 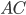 и
и 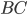 . Найдите угол
. Найдите угол 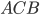 . Ответ дайте в градусах (см. рис. 3).
. Ответ дайте в градусах (см. рис. 3).
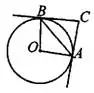
Решение.
 , так как касательная перпендикулярна радиусу, проведённому в точку касания.
, так как касательная перпендикулярна радиусу, проведённому в точку касания.  (центральный угол опирается на дугу 56°). В четырёхугольнике
(центральный угол опирается на дугу 56°). В четырёхугольнике  сумма углов равна 360°.
сумма углов равна 360°. 
Ответ: 124.
Задача 4. Найдите величину угла 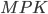 . Ответ дайте в градусах (см. рис. 4).
. Ответ дайте в градусах (см. рис. 4).
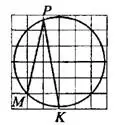
Решение.
При формулировании подобных задач имеется в виду, что отмеченная на рисунке дуга 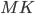 меньше всей окружности в целое число раз.
меньше всей окружности в целое число раз.
Дуга  — одна четвёртая всей окружности (см. рис. 5),
— одна четвёртая всей окружности (см. рис. 5),  — одна восьмая, то есть 360° : 8 = 45°. Вписанный
— одна восьмая, то есть 360° : 8 = 45°. Вписанный  опирается на дугу
опирается на дугу  , значит
, значит

Ответ: 22,5.
Задача 5. Центральный угол на 54° больше острого вписанного угла, опирающегося на ту же дугу окружности (см. рис. 6). Найдите вписанный угол. Ответ дайте в градусах.
Решение.
Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу. Если он на 54° больше вписанного угла, то вписанный угол равен 54°.
Ответ: 54.
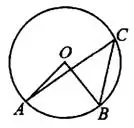
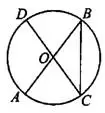
Задача 6. В окружности с центром 
 и
и  — диаметры (см. рис. 7). Центральный угол AOD равен 108°. Найдите вписанный угол рис j^g ABC. Ответ дайте в градусах.
— диаметры (см. рис. 7). Центральный угол AOD равен 108°. Найдите вписанный угол рис j^g ABC. Ответ дайте в градусах.
Решение.
Диаметр  опирается на полуокружность
опирается на полуокружность 
 Вписанный угол
Вписанный угол  равен половине угловой величины дуги, на которую опирается.
равен половине угловой величины дуги, на которую опирается. 
Ответ: 36.
Задача 7. Найдите угол  , если вписанные углы
, если вписанные углы  и
и  опираются на дуги окружности, градусные величины которых равны соответственно 106° и 42° (см. рис. 8). Ответ дайте в градусах.
опираются на дуги окружности, градусные величины которых равны соответственно 106° и 42° (см. рис. 8). Ответ дайте в градусах.
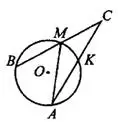
Решение.
Вписанный угол равен половине градусной меры дуги, на которую он опирается. 
 — внешний к углу
— внешний к углу 
 , значит,
, значит,  равен сумме
равен сумме  и
и  этого треугольника.
этого треугольника. 
Ответ: 32.
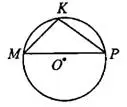
Задача 8. Хорда  делит окружность на две части, градусные величины которых относятся как 4 : 8. Под каким углом видна эта хорда из точки
делит окружность на две части, градусные величины которых относятся как 4 : 8. Под каким углом видна эта хорда из точки 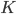 , принадлежащей меньшей дуге
, принадлежащей меньшей дуге 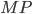 ? Ответ дайте в градусах (см. рис. 9).
? Ответ дайте в градусах (см. рис. 9).
Решение.
 — вписанный, он равен половине дуги
— вписанный, он равен половине дуги 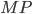 , на которую он опирается. Окружность 360° делится на две части, которые относятся как 4 : 8, обозначим эти части 4х и 8х. 4х + 8х = 360, 12x = 360, х = 360 : 12 = 30, большая дуга 8х = 8 • 30 = 240.
, на которую он опирается. Окружность 360° делится на две части, которые относятся как 4 : 8, обозначим эти части 4х и 8х. 4х + 8х = 360, 12x = 360, х = 360 : 12 = 30, большая дуга 8х = 8 • 30 = 240. 
Ответ: 120.







