Углы, связанные с окружностью (теория). Готовимся к ЕГЭ по математике. Геометрия. Урок 14

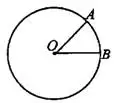
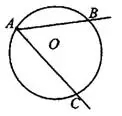
Угол с вершиной в центре окружности называется центральным углом.
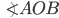$O$ — центр окружности, $\displaystyle \angle AOB$ — центральный угол, опирающийся на дугу 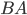$BA$ (см. рис. 1).

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
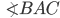Точки $A, B, C$ лежат на окружности, следовательно, $\displaystyle \angle BAC$ — вписанный угол, опирающийся на дугу 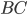$BC$ (см. рис. 2).

1°. Центральный угол равен величине дуги, на которую он опирается.
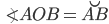$O$ — центр окружности, $A$ и $B$ лежат на окружности. $\displaystyle \angle AOB=\breve{AB}$ (см. рис. 1).
2°. Вписанный угол равен половине угловой величины дуги, на которую он опирается.
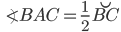$\displaystyle \angle BAC=\frac{1}{2}\breve{BC}$ (см. рис. 2).
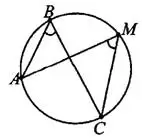
3°. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
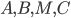$A, B, M, C$ лежат на окружности. $\displaystyle \angle ABC=\angle AMC$ (см. рис. 3).

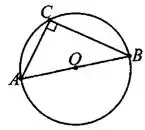
4°. Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90° (см. рис. 4).

5°. Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.
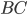$BA$ — хорда, $BC$ — касательная, следовательно, 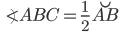$\displaystyle \angle ABC=\frac{1}{2}\breve{AB}$ (см. рис. 5).

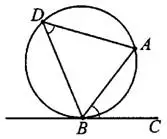
6°. Угол между касательной и хордой равен вписанному углу, который опирается на дугу, заключённую между касательной и хордой.
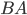$BA$ — хорда, 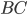$BC$ — касательная, следовательно, 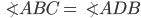$\displaystyle \angle ABC=\angle ADB$ (см. рис. 5).