График функции корня. Готовимся к ОГЭ по математике. Модуль 1. Урок 40

Рассмотрим графики функций квадратного и кубического корней. Областью определения функции, заданной формулой $\displaystyle y=\sqrt{x}$, является $\displaystyle x\geq 0$. Областью определения функции, заданной формулой $\displaystyle y=\sqrt[3]{x}$, являются все действительные числа (см. рис. 1).

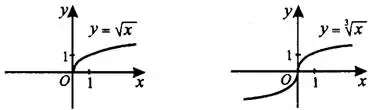
Рис.1

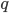График функции, заданной формулой вида $\displaystyle y=\sqrt{x-p}+q$, получается из графика, заданного формулой $\displaystyle y=\sqrt{x}$, параллельным переносом вправо вдоль оси $Ox$ на $p$ и вверх вдоль оси $Oy$ на $q$. Например, график функции $\displaystyle y=\sqrt{x-2}+1$ получается из графика $\displaystyle y=\sqrt{x}$ параллельным переносом вправо на 2 деления и вверх на 1 (см. рис. 2).

Рис.2

Пример 1. Установите соответствие между графиками функций (см. рис. 3) и формулами, которые их задают.
1) $\displaystyle y=\sqrt{x}$; 2) $\displaystyle y=\sqrt{x}-3$; 3) $\displaystyle y=\sqrt{x+3}$; 4) $\displaystyle y=\sqrt{x+1}$.

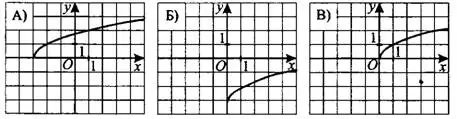
Рис.3

Решение. Заметим, что графики А — В представляют собой смещённые графики функции $\displaystyle y=\sqrt{x}$, а потому задаются формулами вида $\displaystyle y=\sqrt{x-p}+q$.
График А проходит через (-3; 0) и задаётся формулой $\displaystyle y=\sqrt{x+3}$, так как из предложенных только она удовлетворяет соотношению $y(-3)=0$.
График Б проходит через (0; -3) и задаётся формулой $\displaystyle y=\sqrt{x}-3$, так как из предложенных только она удовлетворяет соотношению $y(0)=-3$.
График В проходит через (0;0) и задаётся формулой $\displaystyle y=\sqrt{x}$, так как из предложенных только она удовлетворяет соотношению $y(0)=0$.
Ответ: А-3; Б-2; В-1.
Замечание. Вообще говоря, подстановка координат одной точки в формулы может оказаться недостаточной (несколько формул превратятся в верные равенства). Тогда надо подставить координаты ещё одной точки.