График функции, заданной формулой вида  или
или  ,
,  , — гипербола.
, — гипербола.
Область определения функции, заданной формулой  , — все действительные числа, кроме 0, значит, график этой функции не пересекает ось ординат. Аналогично график, заданный
, — все действительные числа, кроме 0, значит, график этой функции не пересекает ось ординат. Аналогично график, заданный  , не будет проходить ни через одну точку плоскости с абсциссой
, не будет проходить ни через одну точку плоскости с абсциссой 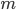 (то есть не пересекает вертикальную прямую
(то есть не пересекает вертикальную прямую  ).
).
В зависимости от значений, которые принимают параметры 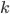 , гипербола
, гипербола  - может быть по-разному расположена на декартовой плоскости. При гипербола расположена в I и III четвертях, при
- может быть по-разному расположена на декартовой плоскости. При гипербола расположена в I и III четвертях, при  — во II и IV (см. рис. 1).
— во II и IV (см. рис. 1).
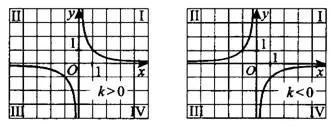
Рис.1
При наличии параметров 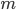 и
и  график гиперболы получается из графика
график гиперболы получается из графика  параллельным переносом вправо вдоль оси
параллельным переносом вправо вдоль оси  на
на 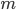 и вверх вдоль оси
и вверх вдоль оси  на
на  (см. рис. 2).
(см. рис. 2).
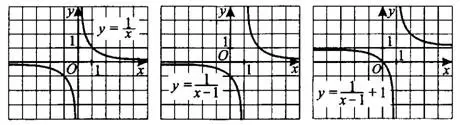
Рис.2
Пример 1. Установите соответствие между графиками функций (см. рис. 3) и формулами, которые их задают.
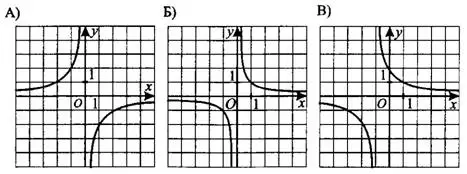
Рис. 3
1)  ; 2)
; 2)  ; 3 )
; 3 )  ; 4)
; 4)  .
.
Решение. Все три графика — гиперболы, то есть заданы формулами вида  или
или  .
.
Для графика А значение параметра  , значит, он может быть задан формулами 1 или 4. Проверим точку (1; -2), через которую проходит этот график. Формула номер 1:
, значит, он может быть задан формулами 1 или 4. Проверим точку (1; -2), через которую проходит этот график. Формула номер 1:  — подходит. Формула номер 4:
— подходит. Формула номер 4:  — не подходит. Следовательно, из предложенных формул графику А соответствует формула 1. Для графика Б выполняется , значит, он может быть задан формулами 2 или 3. Проверим точку (—1;-1), через которую проходит этот график (точку (1; 1) брать нецелесообразно, так как график В также проходит через неё). Формула 2:
— не подходит. Следовательно, из предложенных формул графику А соответствует формула 1. Для графика Б выполняется , значит, он может быть задан формулами 2 или 3. Проверим точку (—1;-1), через которую проходит этот график (точку (1; 1) брать нецелесообразно, так как график В также проходит через неё). Формула 2:  — не определено, поэтому не подходит.
— не определено, поэтому не подходит.
Формула 3:  — подходит. Следовательно, из предложенных формул графику Б соответствует формула 3.
— подходит. Следовательно, из предложенных формул графику Б соответствует формула 3.
Для графика В выполняется , значит, он может быть задан формулами 2 или 3. Так как из них неиспользованной осталась только формула 2, то она и задаёт этот график.
Ответ: А-1; Б-3; В-2.







