График функции - прямая. Готовимся к ОГЭ по математике. Модуль 1. Урок 37

График функций, заданных формулой вида $\displaystyle y=kx+b$ , — прямая.
Рассмотрим разные случаи расположения прямой в зависимости от значений коэффициентов 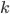$k$ и $b$ в формуле (см. рис. 1).

Рис. 1

Коэффициент $k$ определяет угол наклона прямой. При $k=0$ функция имеет вид $\displaystyle y=b$ , её график параллелен оси абсцисс (оси $Ox$ ). При $\displaystyle k>0$ прямая уходит вправо и вверх: при возрастании $x$ значение функции $\displaystyle y=kx+b$ также возрастает. При $\displaystyle k< 0$ прямая уходит вправо и вниз: при возрастании $x$ значение функции $\displaystyle y=kx+b$ убывает. Коэффициент $b$ определяет, в каком месте график пере сечёт ось ординат (ось $Oy$ ). При $b=0$ получаем функцию $\displaystyle y=kx$ . Её график — прямая, проходящая через начало координат. Действительно, точка (0; 0) принадлежит графику функции $\displaystyle y=kx$ , так как $\displaystyle 0=k\cdot 0$ . 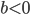При $b>0$ функция пересекает ось ординат выше оси абсцисс, а при $b<0$ — ниже оси абсцисс. Действительно, точке пересечения графика и оси ординат соответствует точка графика с абсциссой $x=0$ , то есть точка $(0;b)$ . В зависимости от знака $b$ эта точка находится выше или ниже оси абсцисс.
Пример 1. Установите соответствие между графиками функций (см. рис. 2) и формулами, которые их задают.

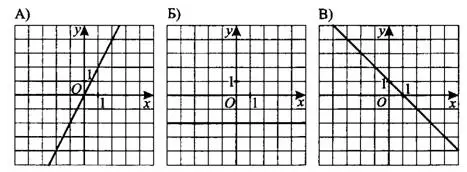
Рис. 2

1) $\displaystyle y=-2x+1$ ; 2) $\displaystyle y=2x$ ; 3) $\displaystyle y=-x+1$ ; 4) $\displaystyle y=-2$ .
Решение. Все три графика — прямые, то есть заданы формулами вида $\displaystyle y=kx+b$ .
Для графика А выполняется $b=0$ , так как прямая проходит через начало координат. Из предложенных вариантов ему соответствует формула $\displaystyle y=2x$ (2).
График Б параллелен оси абсцисс, поэтому $k=0$ , из предложенных вариантов ему соответствует формула $\displaystyle y=-2$ (4). Для В выполняется $k<0$ и $b>0$ , то есть ему могут соответствовать формулы $\displaystyle y=-2x+1$ (1) или $\displaystyle y=-x+1$ (3). Найдём подходящую формулу по двум точкам. График В проходит через точки плоскости с координатами (0; 1) и (1; 0). Подставим в формулы значения координат этих точек: для формулы 1 получаем при $x=0, y=0+1=1$ ; при $x=1, y=-2+1=-1$ , ей график соответствовать не может. Для формулы 3 получаем: $x=0, y=0+1=1$ ; при $x=1, y =-1+1=0$ , следовательно, график В соответствует формуле 3.
Ответ: A-2, Б-4, В-3.
Замечание. Любая прямая задаётся двумя точками, поэтому для проверки соответствия формулы и графика достаточно подставить в формулу координаты двух точек графика (при условии, что формула задаёт прямую и график является тоже прямой).