Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны. На рисунке 1  — параллелограмм, так как
— параллелограмм, так как  и
и  .
.
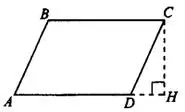
Рис. 1
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию:  (см. рис.1).
(см. рис.1).
Площадь параллелограмма равна произведению двух его сторон на синус угла между ними:  (см. рис.1).
(см. рис.1).
Свойства:
1) Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°. То есть  и
и  (см. рис.1).
(см. рис.1).
2) В параллелограмме противоположные стороны равны, то есть  (см. рис.1).
(см. рис.1).
3) В параллелограмме противоположные углы равны, то есть  (см. рис.1).
(см. рис.1).
4) Диагонали параллелограмма точкой пересечения делятся пополам, т. е.  (см. рис.2).
(см. рис.2).
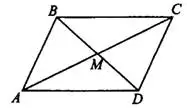
Рис.2
Признаки параллелограмма
1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм. То есть, если  и
и  , то
, то  — параллелограмм (см. рис.3).
— параллелограмм (см. рис.3).
2) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник — параллелограмм. То есть, если  и
и  , то
, то  — параллелограмм (см. рис.3).
— параллелограмм (см. рис.3).
3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
Рис.3
Задача 1. В четырёхугольнике 
 . Найдите
. Найдите  , если
, если  (см. рис.4).
(см. рис.4).
Рис.4
Решение.
Так как  , то
, то  по признаку параллельных прямых. Тогда
по признаку параллельных прямых. Тогда 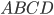 — параллелограмм. (
— параллелограмм. ( — первый признак параллелограмма). Значит, по свойству 4) параллелограмма получаем
— первый признак параллелограмма). Значит, по свойству 4) параллелограмма получаем 
Ответ: 4.
Задача 2. Найдите площади параллелограммов, изображённых на рисунке 5, если величина клетки равна 1.
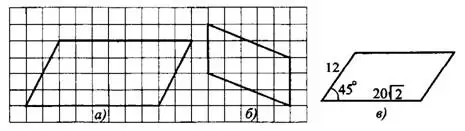
Рис.5
Решение.
Проведём высоты в параллелограммах а) и б) (см. рис.6) и по клеточкам посчитаем их основания  и высоты
и высоты 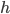 . После этого вычислим площадь
. После этого вычислим площадь 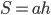 .
.
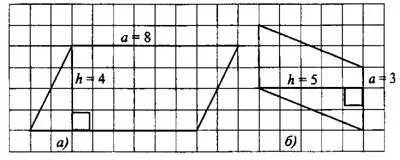
Рис.6
а) 
б) 
в) Вычислим площадь по формуле:  , где
, где  .
.

Ответ: а) 32, б) 15, в) 240.







