Площадь треугольника равна половине произведения любой его стороны на высоту, проведённую к этой стороне:  (см. рис. 1).
(см. рис. 1).
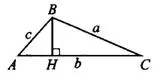
Рис.1
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:  (cм. рис.1).
(cм. рис.1).
Треугольники с равной площадью называются равновеликими.
Площадь прямоугольного треугольника равна половине произведения катетов:  (см. рис.2).
(см. рис.2).
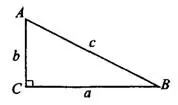
Рис.2
Если  и
и  ,
,
то 
Задача 1. Найдите площадь треугольника, изображённого на рисунке 3.
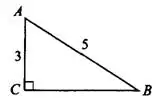
Рис.3
Решение.
По теореме Пифагора  ,
,

Ответ: 6.
Задача 2. Найдите площади треугольников, изображённых на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.4). Ответ дайте в квадратных сантиметрах.
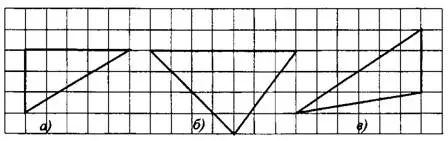
Рис.4
Решение.
а) Треугольник является прямоугольным. По рисунку катеты равны 3 и 5, площадь 
Проведём высоты на рисунках б) и в) (см. рис. 5).
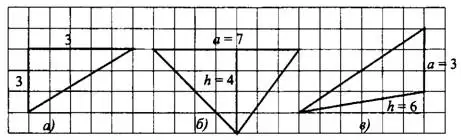
Рис.5
Найдём площадь 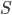 по формуле
по формуле  .
.
б)  ; в)
; в)  .
.
Ответ: а) 7,5, б) 14, в) 9.
Задача 1. Найдите площадь  , изображённого на рисунке 6.
, изображённого на рисунке 6.
Решение.
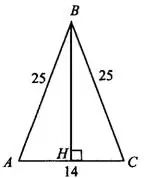
Рис.6
 - равнобедренный, высота
- равнобедренный, высота 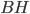 является медианой, то есть
является медианой, то есть  .
.
Найдём высоту 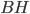 из прямоугольного
из прямоугольного  .
.


Ответ: 168.







